006 - 締まっていこう

平らな板に2つの穴が開けられている．板の表側には何本もの針が刺してある．1本のひもが裏側から穴の1つを通して表側に出ており，板の表面を折れ線状に曲がりながら，もう1つの穴に達し，そこから裏側に抜けている．この時点では，ひもは針に触れていない．

図F-1, F-2, F-3は穴，針およびひもの配置の例をそれぞれ示している．白い四角と円はそれぞれ穴と針を表している．ひもは実線で表された折れ線である．

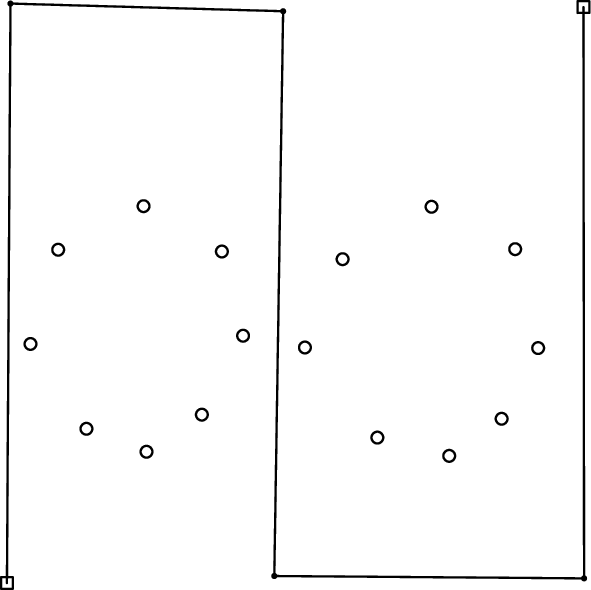
図F-1: 穴，針，ひもの配置例

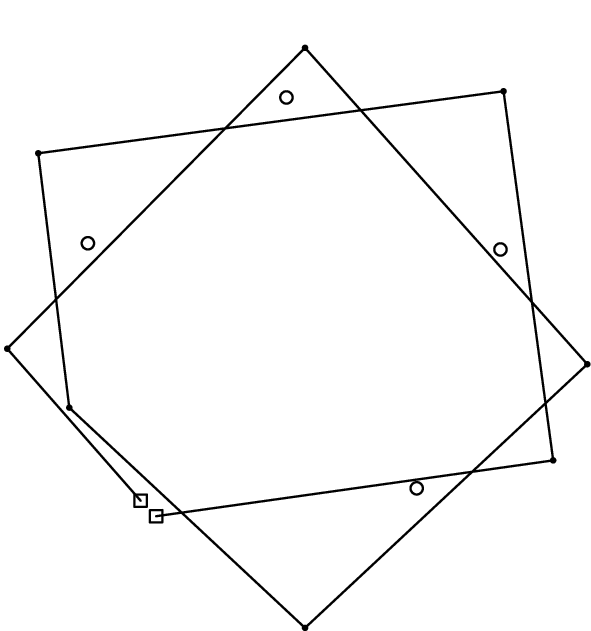
図F-2: 穴，針，ひもの配置例

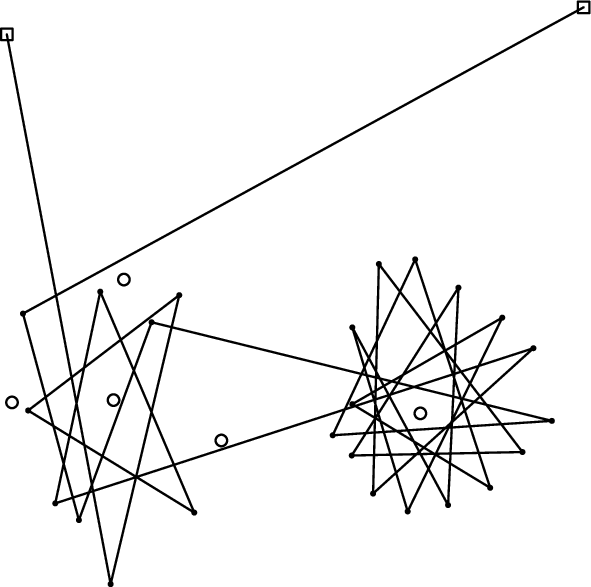
図F-3: 穴，針，ひもの配置例

いま，ひもの両端に同じ重さの石を取り付けたところ，ひもはゆっくりと変形して緩みのない状態になった．このとき，いくつかの針にひっかかり，最初とは異なる折れ線状になった．(ただし，1つの針にもひっかからないこともある．)

変形の際，ひもはそれ自身にひっかかることはないものとする．つまり，ひもの緩みがなくなったとき，ひもはいくつかの針の位置を頂点，2つの穴の位置を端点とするような折れ線を板の表面上に描く．例えば図F-1, F-2, F-3の配置からは，それぞれ図F-4, F-5, F-6の折れ線が得られる．この折れ線の全長を求めるプログラムを作成せよ．

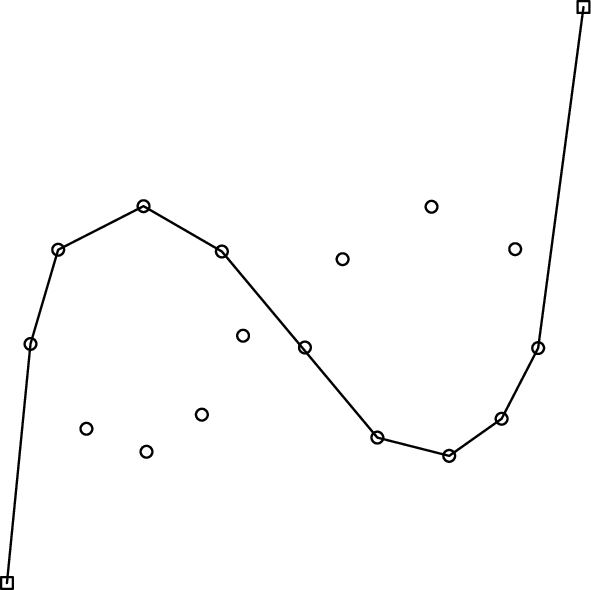
図F-4: 図F-1の配置からひもの緩みをなくした状態

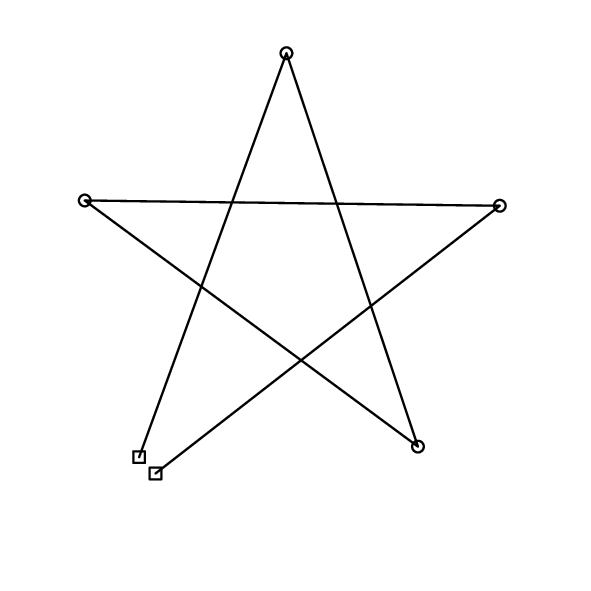
図F-5: 図F-2の配置からひもの緩みをなくした状態

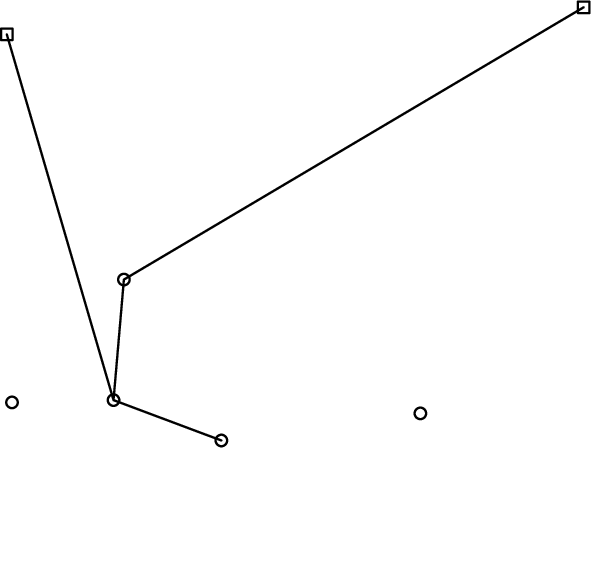
図F-6: 図F-3の配置からひもの緩みをなくした状態

ただし，ひも，針，穴の直径は無視できるほど小さいものとする．

入力は複数のデータセットから成り，最後に2つのゼロが空白で区切られた行が続く．1つのデータセットは以下の形式でひもの初期形状(穴および頂点の位置)と針の位置を与える．

m n
x₁ y₁
...
x_l y_l

1行目は2つの整数 m, n (2 ? m ? 100, 0 ? n ? 100)で，ひもの初期形状を表す両端の穴を含む頂点数(m)と針の本数(n)とを表している．続く l = m + n 行の各行は2つの整数 x_i , y_i (0 ? x_i ? 1000, 0 ? y_i ? 1000) によって平面上の座標 P_i = (x_i , y_i ) を表している．

• P₁ から P_m まではひもの初期形状を表す．つまり，P₁ と P_m にはひもが通っている穴があいており，ひもは P_i (i = 1, ..., m)を順に通る折れ線状になっている．
• P_m+1 から P_m+n まではn本の針の位置を表している．

ただし，2つの座標が同じ位置にあることはない．また，3つの座標が直線上に並ぶことはないとする．

各データセットについて，ひもの緩みがなくなったときの板の表面上に残されたひもの部分の長さが書かれた1行を出力せよ．1つの出力行は余計な文字を含んではならない．

出力される長さは 0.001 より大きな誤差を持ってはならない．

6 16
5 4
11 988
474 975
459 16
985 12
984 982
242 227
140 266
45 410
92 570
237 644
370 567
406 424
336 290
756 220
634 251
511 404
575 554
726 643
868 571
907 403
845 283
10 4
261 196
943 289
859 925
56 822
112 383
514 0
1000 457
514 1000
0 485
233 224
710 242
850 654
485 915
140 663
26 5
0 953
180 0
299 501
37 301
325 124
162 507
84 140
913 409
635 157
645 555
894 229
598 223
783 514
765 137
599 445
695 126
859 462
599 312
838 167
708 563
565 258
945 283
251 454
125 111
28 469
1000 1000
185 319
717 296
9 315
372 249
203 528
15 15
200 247
859 597
340 134
967 247
421 623
1000 427
751 1000
102 737
448 0
978 510
556 907
0 582
627 201
697 963
616 608
345 819
810 809
437 706
702 695
448 474
605 474
329 355
691 350
816 231
313 216
864 360
772 278
756 747
529 639
513 525
0 0

2257.0518296609
3609.92159564177
2195.83727086364
3619.77160684813