006 - 宗教戦争
時間制限 1 秒 / メモリ制限 256 MB / 得点 100 / x 0 /
果たしてここまで来たか。
腹立たしいまでに優秀である。
だがもっとも望ましい形に進んできているのはとても愉快だ。
我が正答零人素敵計画は
君らの強い誤答を以って
ついに完遂されることとなる。
いよいよもって死ぬがよい。
そしてさようなら。
問題
ここは魔術大国Grimwar。 魔法により統治された平和な国である。
しかし今日、この国に隣国の NOW_MAN_ZAW が攻めてくるという情報が入った。
NOW_MAN_ZAW は、 『力のコーヒー』 と呼ばれる薬を服用しており、
昼夜絶えず活動を行うことが可能であるという。
しかし Grimwar の住民は、昼夜絶えず活動を行うことができない。
これはいけない。
そこでGrimwarを統べる姫 Alice は、NOW_MAN_ZAWの侵攻を防ぐため、
他の魔導師の力を借り、国に防御結界を張ることにした。
結界は国の中の各都市にある魔法陣を頂点として張ることができる。
結界は全ての都市を内包してなければならない。
一つの魔法陣に一人の魔導師が必要となるため、
結界を張るのに使用する魔法陣の数は最小にしたい。
結界の辺上に、都市が有っても良い。
つまり、結界の辺が座標(1,1) と、座標(1,3) を繋いでいた場合、
座標(1,2) に都市があっても、これは結界の頂点として使わなくても良い。
早速結界を張ったAlice達だが、彼女たちは一日に一度疲れてしまう。
そこで電脳世界から 雛ちゃん を呼び寄せた。
彼女は魔導師達の疲労を回復させることが可能であるため、
一日に結界を張っている魔法陣のある都市全てを結界の辺が繋がっている順に
魔法陣のあるどこかの都市から一度ずつ巡回し、
魔導師達の疲労を回復させる役目を受けた。
都市間を移動するのには、都市間の絶対距離分の時間がかかるのだが、
ある都市同士には相互に時間 0 で瞬間移動が可能なリンクラインが繋がれているものがある。
つまり、ある二つの都市間を移動する場合、リンクラインの存在により、
時間がかからない場合がある。
例えば、都市Aから都市Cに移動する場合、
都市Aと都市Bに、都市Bと都市Cにリンクラインが存在する場合、
移動する際の時間はかからない。
ただし、都市A から 都市B に移動しようとし、
都市A と 都市Cにリンクラインが張られており、
都市A から 都市B までの絶対距離よりも、
都市C から 都市B までの絶対距離が短い場合でも、
雛ちゃんは都市A から 都市B までの絶対距離分の時間を必要とする。
つまり、都市A から 都市B までのリンクラインが繋がっていない場合は、
必ず都市A から 都市B までの絶対距離分の時間が必要となる。
リンクラインは、Aliceの尽力により、一日に一つ追加されていく。
雛ちゃんは、その日のリンクラインの完成後に移動を開始するものとする。
Grimwarの都市の情報と、最初から存在するリンクラインの情報、
戦いの日数、各日において追加されるリンクラインの情報が与えられるので、
各日において雛ちゃんが結界を張っている都市を全て訪ね
最初の都市に戻るのに必要な時間を出力せよ。
入力形式
一行目に、都市の数 N 、最初から存在するリンクラインの数 M 、
戦いが続く日数 T が空白区切りで与えられる。
続いてN行にかけて、都市1から都市Nの座標 X , Y が空白区切りで与えられる。
続いてM行にかけて、最初から存在するリンクラインがどの都市を繋いでいるかを示す情報 A , B が空白区切りで与えられる。
続いてT行にかけて、1日目からT日目に追加されたリンクラインがどの都市を繋いでいるかを示す情報 C , D が空白区切りで与えられる。
N M T X1 Y1 X2 Y2 .. .. XN YN A1 B1 A2 B2 .. .. AM BM C1 D1 C2 D2 .. .. CT DT
出力形式
全ての A , B の入力後に、一日目以前の雛ちゃんが
結界を張っている都市を全て訪ね最初の都市に戻るのに必要な時間を改行込みで出力し、
C , D の入力毎に、その日に雛ちゃんが
結界を張っている都市を全て訪ね最初の都市に戻るのに必要な時間を改行込みで出力せよ。
制約
- 入力される値は全て符号付き32ビットに収まる整数である。
- 3 ≦ N ≦ 1,000
- 0 ≦ M ≦ min(N*(N-1)/2,10,000)
- 0 ≦ T ≦ min(N*(N-1)/2 - M , 200,000)
- -100,000,000 ≦ X,Y ≦ 100,000,000
- 1 ≦ A,B,C,D ≦ N
部分点
- M = T = 0
- N , T ≦ 100
入出力例
入力例一
5 1 2 1 1 1 5 2 4 5 1 5 5 1 4 1 3 2 3
出力例一
12.000000 12.000000 8.000000
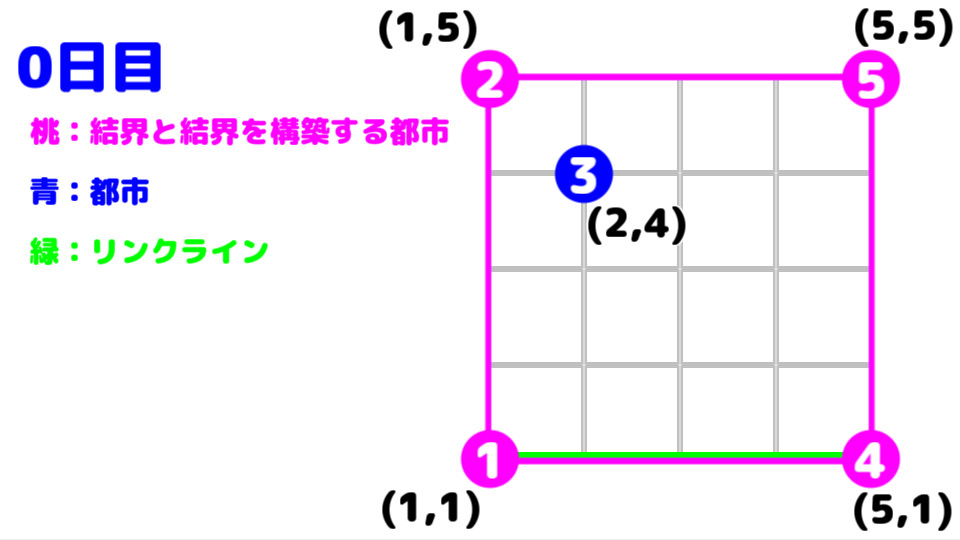
この入力例では、結界は都市 1 , 2 , 5 , 4 の順に張られる。
都市 1 , 2 , 4 , 5 間の絶対距離は共に4である。
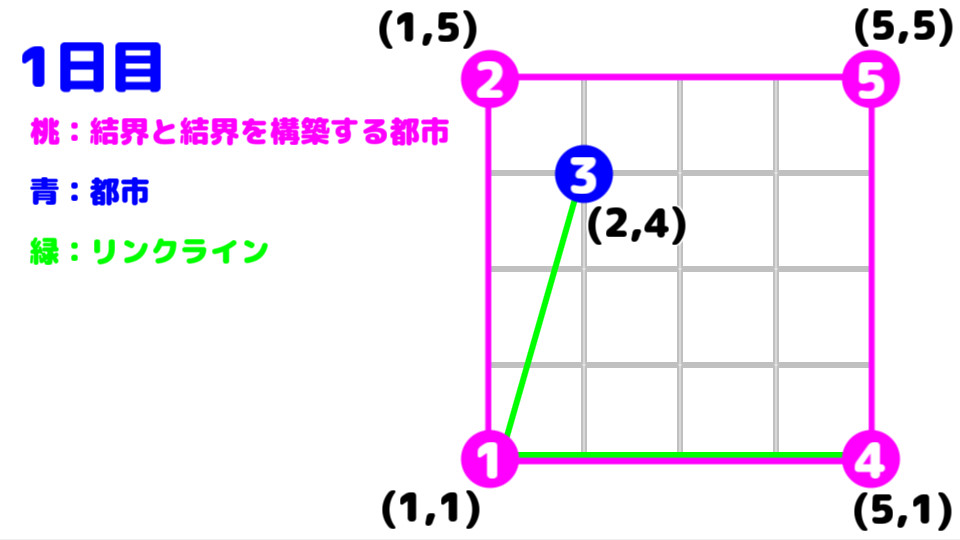
一日目以前は、都市1と都市4が繋がっているため、
その分の移動時間は発生しない。
そのため、一日目以前の総移動時間は "12" となる。
一日目は、都市1と都市4が繋がっているため、
その分の移動時間は発生しない。
そのため、一日目の総移動時間は "12" となる。
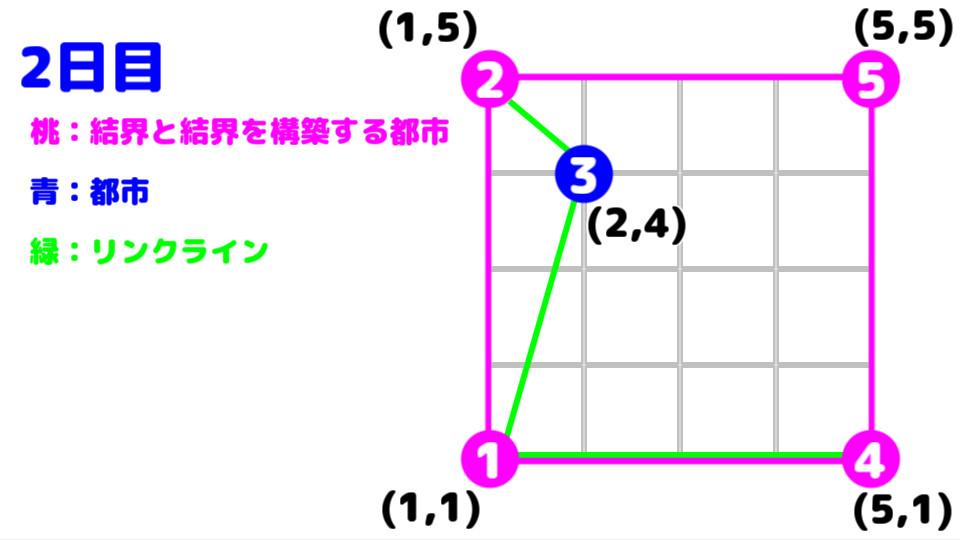
二日目は、都市1と都市4に加え、
都市1と都市2が都市3を経由して繋がっている。
そのため、二日目の総移動時間は "8" となる。
入力例二
6 2 2 -2 0 0 2 2 0 0 -2 -1 0 1 0 1 5 3 6 5 6 2 6
出力例二
11.313708 11.313708 5.656854
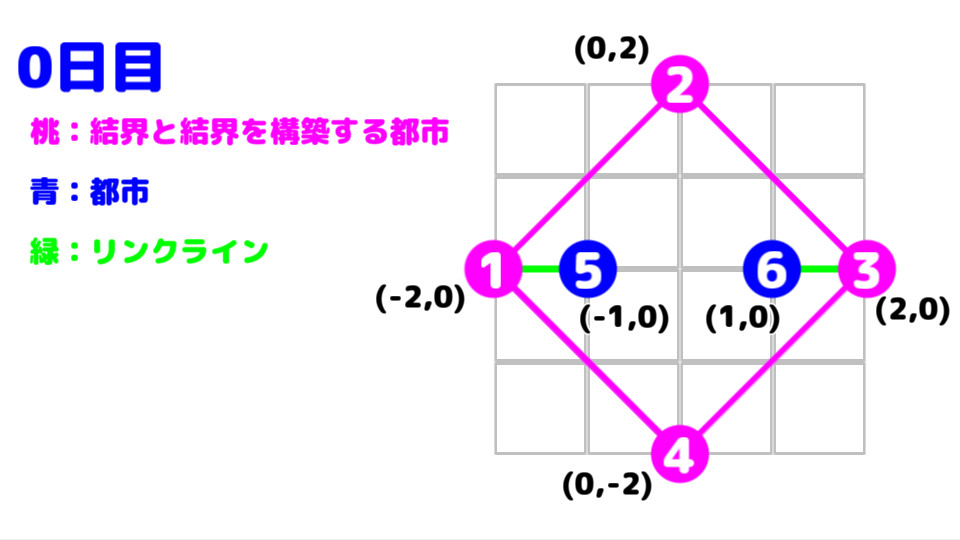
この入力例では、結界は都市 1 , 2 , 3 , 4 の順に張られる。
都市 1 , 2 , 3 , 4 間の絶対距離は共に1.41421356...である。
一日目以前は、結界を張る隣り合った都市同士で繋がっている箇所がないため、
一日目以前の総移動時間は "11.313708" となる。
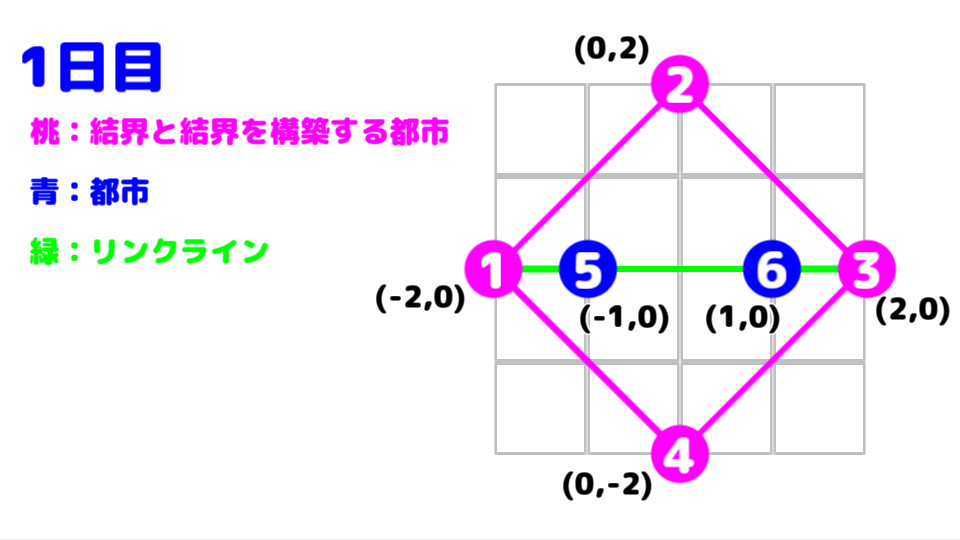
一日目も、結界を張る隣り合った都市同士で繋がっている箇所がないため、
一日目の総移動時間は "11.313708" となる。
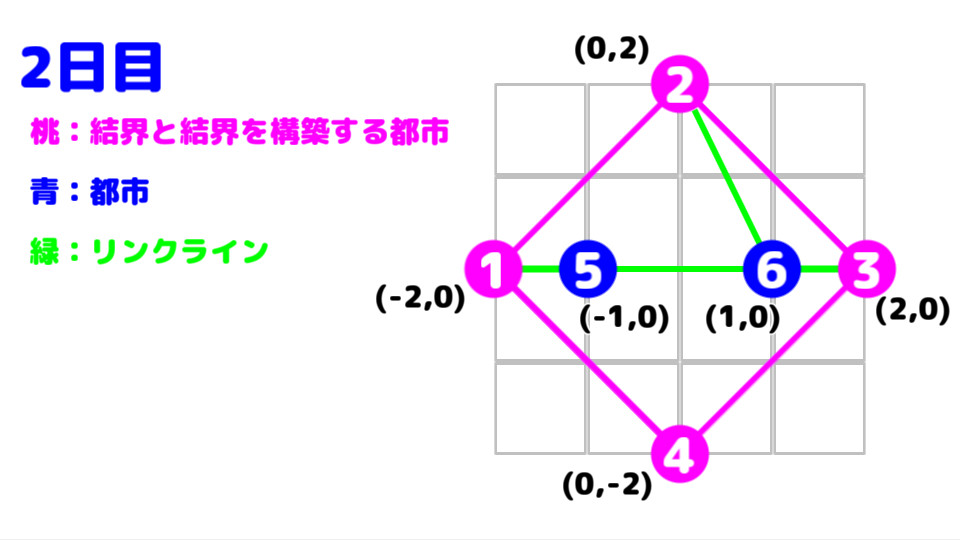
二日目は、都市 1 , 2 , 3 が都市 5 , 6 を経由して繋がっているため、
都市1から都市2、そして都市2から都市3への移動時間は発生しない。
よって二日目の総移動時間は "5.65854" となる。
入力例三
3 0 1 1 1 4 5 1 4 1 2
出力例三
11.162278 6.162278
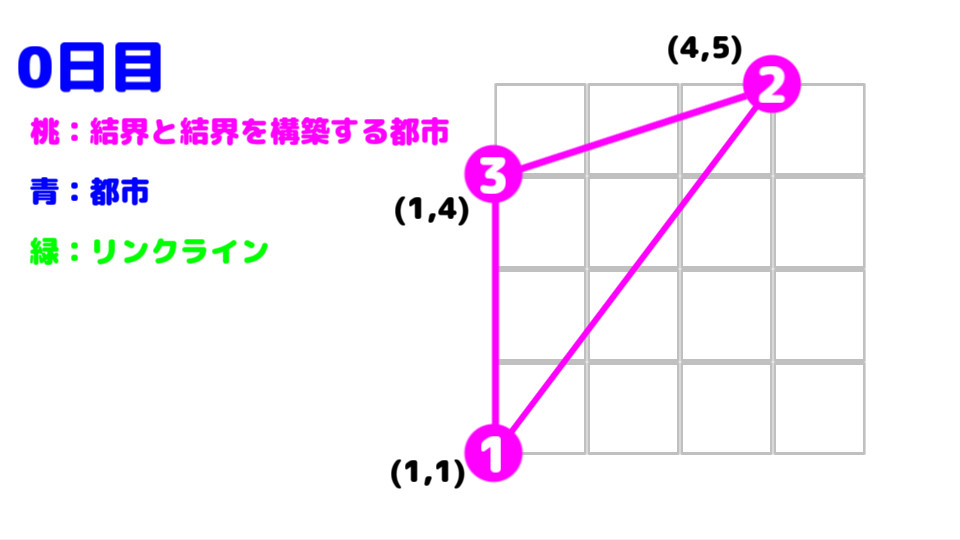
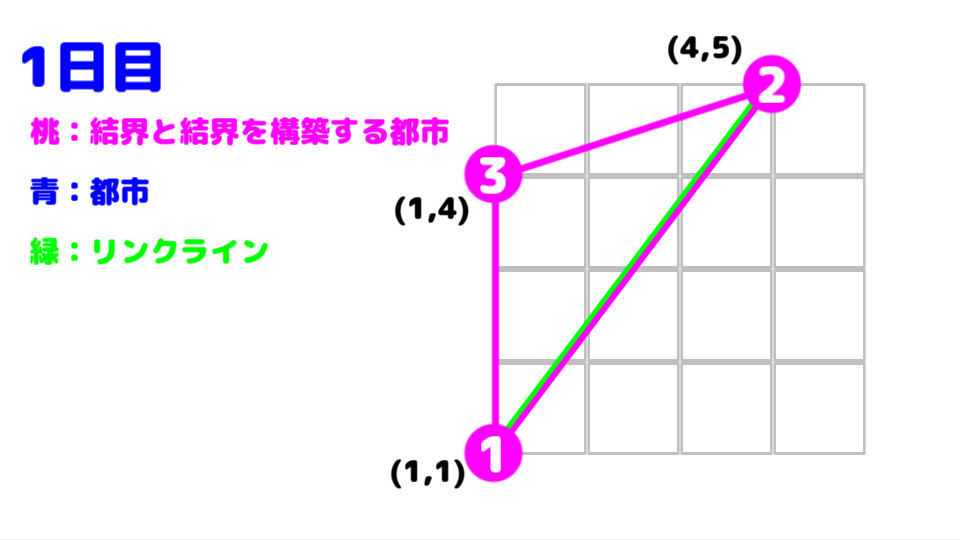
この入力例では、結界は、都市 1 , 2 , 3 の順に張られる。
都市 1 , 2 間の距離は 5 ,
都市 2 , 3 間の距離は 3.162278... ,
都市 3 , 1 間の絶対距離は 3 である。
一日目以前は、隣り合った都市同士で繋がっている箇所がないため、
一日目以前の総移動時間は、 "11.162278" となる。
一日目は、都市 1 から 都市 2 が繋がっているため、
その分の移動時間は発生しない。
よって一日目の総移動時間は "6.162278" となる。
都市 2 から 都市 3 に移動する際、
一度都市 1 に瞬間移動してから
都市 3 に移動するといったことはできないことに注意せよ。
入力例四
9 0 8 1 1 2 1 3 1 1 2 2 2 3 2 1 3 2 3 3 3 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9
出力例四
8.000000 8.000000 6.000000 6.000000 6.000000 6.000000 4.000000 4.000000 0.000000