003 - Dragon Curve

問題

MMNMMさんは夏祭りで駄菓子を買いました。
駄菓子には長い紙の帯がついていて、MMNMMさんはこれを使って何かフラクタル図形を作ろうと考えました。
長い紙の帯を使って作ることができるフラクタル図形に"ドラゴンカーブ"があります。

ドラゴンカーブとは、次のようにして作られるフラクタル図形です。
①長さ$2^N$の紙の帯を用意し、片方の端を$0$、もう片方の端を$2^N$とするようにそれぞれの端を定める。
②$2^N$の端をもって、$0$の端の上に重なるように二つに折る。
③できあがった長さ$2^{N-1}$の紙の帯の、二つの端が重なったほうの端を$0$、折り目になっているほうの端を$2^{N-1}$とし、長さが$1$でなければ②に戻る。
④できあがった紙の帯を開き、折り目が90°になるように形を整える。



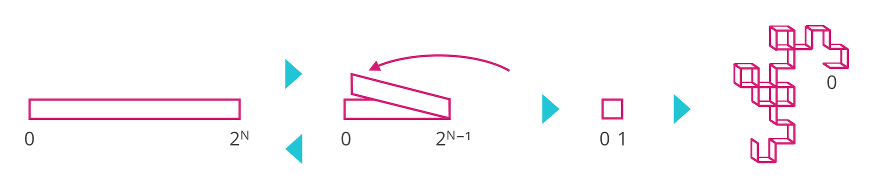
MMNMMさんは紙の帯の$0$の端から距離$d$の折り目が山折りか谷折りかが気になりました。
最初につける折り目は谷折りです。
紙の帯の$0$の端から距離$d$の折り目が山折りか谷折りかを判定してください。

入力

入力は以下の形式で与えられる。

$N\ d$

一行目には整数$N,d$がこの順に空白区切りで与えられる。
$N$は、紙の帯の長さが$2^N$であることを示している。
$d$は、判定するべき折り目の位置を示している。

出力

0の端からの距離が$d$である折り目が山折りならば"YAMA"、谷折りならば"TANI"と一行に出力しなさい。

制約

全てのに入出力ケースついて$N$, $d$はそれぞれ以下の条件を満たす。

• $1\leqq N\leqq10^{18}$
  
• $0\lt d\lt10^{18}$
  
• $d\lt2^N$
  
  

小課題(10点分)の入出力ケースについて以下の条件を満たす。

• $N\leqq20$
  
  

$2^N$が64ビット整数型に収まらない可能性があることに注意しなさい。

入出力例

入力例1

3 3

出力例1

YAMA

折り目は、順番に谷谷山谷谷山山で、3番目の折り目は山折りです。

入力例2

25 114514

出力例2

TANI

入力例3

47 1000000007

出力例3

YAMA

この入力例は小課題の制約を満たしません。