002 - 君も始めようダイクストラ大好き厨

Question.

しょりぶの3年には、ダイクストラ大好き厨四天王が存在している。
3年になった時にこの四天王の中に入るために、君もダイクストラ大好き厨になろう。

ダイクストラ（最短経路問題）とは、1つの始点からあるノードにたどり着くための距離を求めるアルゴリズムである。
以下のような図が想像できる状況なら解法にダイクストラを視野に入れてみるべきだろう。



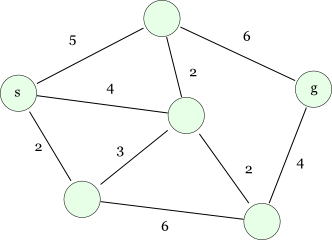
今回は無向グラフ（双方向に移動が可能なグラフ）とする。

以下の情報が与えられる。

ノード(円)の数N, エッジ(線)の数M

エッジが繋ぐ2つのノードa, b, エッジを辿る際のコストc

　この情報を元に、スタート(1)からゴール(N)までの最短コストを求めてみよう。

Input.

N M
a1 b1 c1
.    .    .
.    .    .
.    .    .
am bm cm

1 行目に整数 N M が与えられる。

2 行目から M+1 行目に整数 a b c が与えられる。

Output.

ノード1 からノードN までの最小コストを出力せよ。出力の最後に改行を入れること。
また、ノードN まで行く経路が存在しない場合がある。その際は"NA"と出力せよ。

Constraint.

全ての入出力ケースについて以下を満たす。

• 3 ≦ N ≦ 10⁵
• 4 ≦ M ≦ min(N(N-1), 114514)
• 1 ≦ a, b ≦ N
• 1 ≦ c ≦ 10²

---

Sample input and output.

Sample1 input

6 9
1 2 2
1 3 5
1 4 4
2 4 3
3 4 2
2 5 6
4 5 2
3 6 6
5 6 4

Sample1 output

10

Explanation1.

このサンプルは、上図と同じである。
左から順にノード1~6となっている。

Sample2 input

5 6
1 2 4
2 3 2
2 5 8
3 4 5
1 3 3
3 5 7

Sample2 output

10

Sample3 input

6 7
1 2 2
1 3 5
1 4 4
2 4 3
3 4 2
2 5 6
4 5 2

Sample3 output

NA

Explanation3.

このサンプルは、上図からゴールへのエッジを消したものである。
ゴールまで辿り着けないのでNA。