001 - ほもの君と木と無限ループと

問題

N個の頂点とM本の辺から成る無向グラフがある。
無向グラフの連結成分のうち、閉路を持たないものを木と呼ぶ。
ほものくんは、無向グラフが木であるか確かめたい。
閉路のある無向グラフだと、ほものくんは閉路部分を辿ることしかできなくなり、永遠に抜け出せなくなる。
こものくんと化した貴方は、ほものくんを助けてあげたい。

入力

N M
u1 v1
u2 v2
:
uM vM

• 1行目に頂点の個数N, 辺の本数Mが与えられる。
• N(2 ≦ N ≦ 100), M(1 ≦ M ≦ N×(N−1)×2)
• 2行目からM-1行目まで2頂点 u_i ,v_i を結ぶ辺が与えられる。
• u_i ,v_i(1 ≦ u_i < v_i ≦ N)
• どの2頂点についても、それらを直接結ぶ辺は高々1本しか存在しない。

出力

• 無向グラフの連結成分のうち、木であるもの（閉路を持たないもの）の個数を１行に出力する。
• 改行を忘れないこと。

入出力例

入力例1

8 7
1 2
2 3
2 4
5 6
6 7
6 8
7 8

出力例1

1

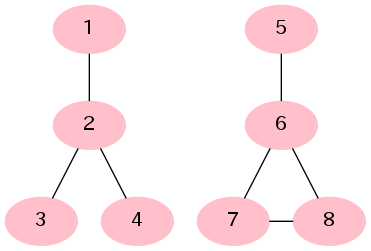
• 左の無向グラフには閉路がない。右の無向グラフには閉路6-7-8-6が含まれている。
• 従って、木であるような連結成分の個数は1である。

入力例2

5 1
1 2

出力例2

4

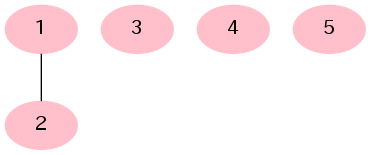
• 1つの頂点からなる連結成分は木とみなされる。

入力例3

11 11
1 2
1 3
2 4
3 5
4 6
5 7
6 8
7 9
8 10
9 11
10 11

出力例3

0

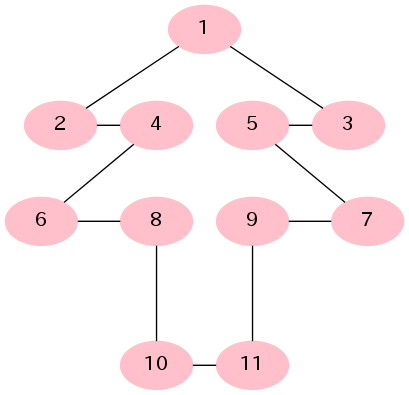
• 木を模したグラフではあるが、ここで言う木とは関係がない。ほものくんは氏ぬ。