005 - 鎖中経路

平面上の複数の円環から構成される鎖がある． 最初（最後）の円は，次（一つ前）の円だけと交差し， 中間の各円は隣の二つの円だけと交差する．

あなたの仕事は，以下の条件を満たす最短経路を見つけることである．

• 経路は，最初と最後の円の中心をつなぐ．
• 経路は鎖中にある．すなわち，経路上のすべての点は，少なくとも一つの円の内側もしくは円周上にある．

図 E-1 は，そのような鎖の例と対応する最短経路を示したものである．

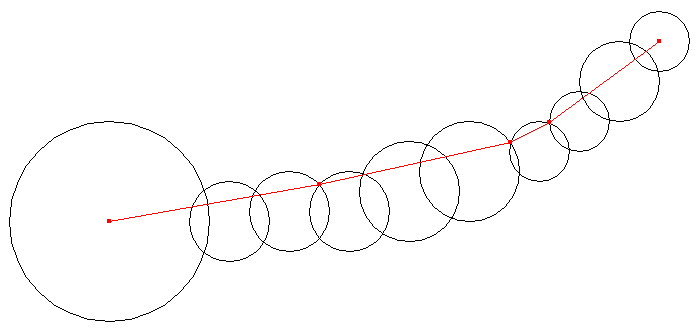
図 E-1: 鎖の例と対応する最短経路

入力は複数のデータセットからなる． 各データセットは一つの鎖の形状を表し，その形式は以下のとおりである．

n
x₁ y₁ r₁
x₂ y₂ r₂
...
x_n y_n r_n

データセットの最初の行は，円の個数を表す整数 n (3 ≤ n ≤ 100) のみからなる． 続く n 行のそれぞれは，空白文字 1 個で区切られた 3 個の整数からなる． (x_i, y_i) と r_i は， i 番目の円 C_i の中心の位置と半径を表す． 0 ≤ x_i ≤ 1000, 0 ≤ y_i ≤ 1000, 1 ≤ r_i ≤ 25 であると仮定してよい．

C_i と C_i+1 (1 ≤ i ≤ n−1) は，離れた 2 点で交差すると仮定してよい． j ≥ i+2 のとき，C_i と C_j は離れており，一方が他方を含むこともない． 加えて，それぞれの円は他の円の中心を内部に含むことがないと仮定してもよい．

入力の終わりは，ゼロを一つだけ含む行で表される．

なお，図 E-1 は，後に示す Sample Input 中の最初のデータセットに対応している． 図 E-2 は，Sample Input 中の引き続くデータセットに対する最短経路を示している．

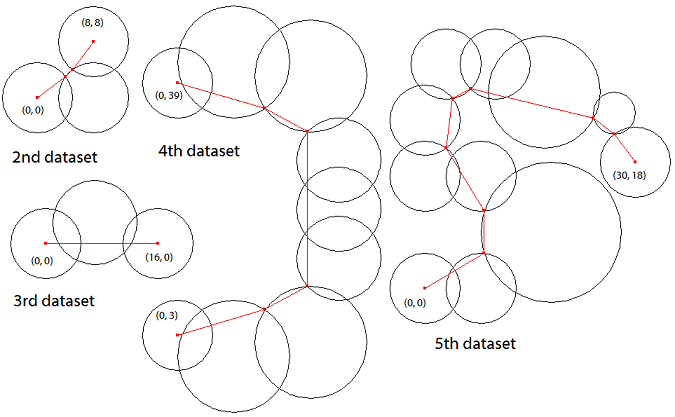
図 E-2: 鎖の例と対応する最短経路

各データセットに対して，最初と最後の円の中心をつなぐ最短鎖中経路の長さを 1 行で出力せよ． 答えには 0.001 を超える誤差があってはいけない． それ以外の余計な文字を出力してはならない．

10
802 0 10
814 0 4
820 1 4
826 1 4
832 3 5
838 5 5
845 7 3
849 10 3
853 14 4
857 18 3
3
0 0 5
8 0 5
8 8 5
3
0 0 5
7 3 6
16 0 5
9
0 3 5
8 0 8
19 2 8
23 14 6
23 21 6
23 28 6
19 40 8
8 42 8
0 39 5
11
0 0 5
8 0 5
18 8 10
8 16 5
0 16 5
0 24 5
3 32 5
10 32 5
17 28 8
27 25 3
30 18 5
0

58.953437
11.414214
16.0
61.874812
63.195179