003 - 避難 (Evacuation)

時間制限 1 秒 / メモリ制限 256 MB / 得点 6 / x 3 /

TLE
1sec
MLE
256MB
得点
6

問題

雛ちゃん王国には $N$ 個の町と $M$ 本の道があります。
各都市には $1 \ldots N$ までの番号が付けられており、都市番号 $n$ の都市を「都市$n$」と呼びます。
$i$本目の道 $(1 \leqq i \leqq M)$ は都市 $s_i$ から $t_i$ を結ぶ一方通行の道で、距離は $c_i$ です。

さて、雛ちゃん王国はYTAによって改装(破壊)されることになったため、全都市の雛ちゃん国民はYDK国へ一時的に避難することになりました。

避難には $K$ 個の都市 $u_1, u_2, ..., u_K$ にあるテレポータを使用します。

各都市の人々はテレポータへたどり着くために、以下の条件に従って都市 $g$ へ行きます。

  • 都市 $g$ にはテレポータがあり、なおかつ自分の都市から最も近い。
  • 都市 $g$ の候補が複数ある場合は、最小の $g$ を選ぶ。
  • 自分の都市までの距離は $0$ とする。
なお、道の整備状況によっては行き先の都市 $g$ が見つからない場合もあります。

テレポータの利用には予約が必要なので、人々はどのテレポータを使うか事前に把握しておきたいです。

そこで、都市$1$ から順に　都市$N$ まで、各都市の行き先の都市 $g$ がどこであるかを求めてください。

入力

N M K
s1 t1 c1
s2 t2 c2
   :
   :
sM tM cM
u1
u2
:
:
uK

一行目に都市の数 $N$、道の数 $M$、テレポータのある都市数 $K$ が与えられ、続く $M$ 行に、道の情報が与えられる。
そして $K$ 行にわたってテレポータのある都市の番号 $u_j$ が与えられる。

出力

都市$1$から順に都市$N$まで、各都市ごとの行き先都市 $g$ を改行区切りで出力せよ。
ただし、行き先の都市 $g$ が見つからない場合は $-1$ を出力すること。

制約

  • 入力される値は全て整数である
  • $1 \leqq N \leqq 100000 \ (10^5) $
  • $0 \leqq M \leqq min \left(3 \times 10^5, \ N \times (N-1) \right) $
  • $1 \leqq K \leqq N $
  • $1 \leqq s,t,u \leqq N $
  • $1 \leqq c \leqq 1000 $
  • $(s_i \neq t_i)$
  • 都市$s_i$ から 都市$t_i$ へ行く道は1本以下である

小課題

  1. [配点の20%] $1 \leqq N \leqq 100$
  2. [配点の80%] 追加の制約はない

入出力例

入力例1

5 5 2
1 2 3
1 4 5
4 5 2
2 3 1
4 2 1
5
3

出力例1

3
3
3
3
5

図にすると以下のようになる。 (緑:テレポータがある都市 )

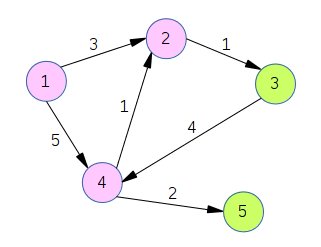
都市$4$については、都市$3$, 都市$5$ のどちらを行き先にしても最短距離が $2$ なので
行き先の候補が2つになるが、このうち最小の番号の都市を選ぶので行き先は都市$3$となる。

入力例2

4 3 1
3 1 4
1 2 1
2 1 1
3

出力例2

-1
-1
3
-1

不運にも道の整備状況が悪いため、都市$1$, 都市$2$, 都市$4$ の人々は改装の惨禍に巻き込まれてしまう。

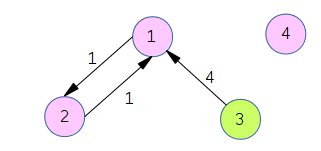
入力例3

11 16 3
2 3 3
2 7 1
3 4 1
4 5 1
7 6 6
8 6 1
5 8 1
1 2 8
1 6 1
5 1 2
4 1 3
3 5 2
9 7 2
9 11 8
10 9 1
10 11 8
11
1
6

出力例3

1
1
1
1
1
6
6
6
6
11
11