004 - 縄張り (Territory)

時間制限 1 秒 / メモリ制限 256 MB / 得点 100 / x 0 /

TLE
1sec
MLE
256MB
得点
100

問題

　あなたは南北方向にとても長く伸びたたくさんの道路と，東西方向にとても長く伸びたたくさんの道路が交わった形をした街に住んでいる．隣り合う 2 つの南北方向の道路の間隔は 1 km である．また，隣り合う 2 つの東西方向の道路の間隔も 1 km である．
　この街には市役所が 1 つある．市役所のある交差点を (0, 0) と表す．この街の交差点は 2 つの整数 i, j を用いて交差点 (i, j) と表される．すなわち，交差点 (i, j) とは，交差点 (0, 0) から東に i km (i < 0 のときは西に -i km)，北に j km (j < 0 のときは南に -j km) 進んだ位置の交差点を表す．
　市役所ではジョイ君という名の 1 匹の犬を飼っている．ジョイ君は K 日間の散歩の計画を立てた．散歩の計画は以下の通りである．

  • K 日のうち最初の日の朝にはジョイ君は交差点 (0, 0) にいる．ジョイ君は交差点 (0, 0) に印を付ける．
  • (0, 0) 以外にはジョイ君が印を付けた交差点はない．
  • K 日のそれぞれの日の昼に散歩を行う．1 日の散歩は N 回のステップからなる．各ステップでは交差点から隣の交差点へと移動し，移動先に印を付ける．ジョイ君がそれぞれの日の昼にどう移動するかは日によらず一定である．
  • 昼の移動が終わった後は，現在いる交差点で次の日の朝まで寝る．

　市役所では K 日間の散歩によってできるジョイ君の縄張りについて話題になっている．4 つの交差点 (a, b), (a + 1, b), (a + 1, b + 1), (a, b + 1) のいずれにもジョイ君が 1 回以上印を付けているとき，4 つの交差点で囲まれた区画はジョイ君の縄張りに属する．
あなたは，ジョイ君の散歩計画から，ジョイ君の縄張りに属する区画の個数を計算するプログラムを作成することとなった．
　この街の道路はとても長く，また，南北方向にも東西方向にも十分たくさんの道路があるため，散歩の途中でジョイ君が道路の端や街の端に到達することはない．

課題

　ジョイ君の散歩計画が与えられると，ジョイ君の縄張りに属する区画の個数を求めるプログラムを作成せよ．

入力

　標準入力から以下の入力を読み込め．

  • 1 行目には 2 個の整数 N, K が空白を区切りとして書かれている．これはそれぞれの日の散歩が N 回のステップからなり，散歩計画が K 日間に渡ることを表している．
  • 2 行目には長さ N の文字列 S が書かれている．文字列 S のうち左から p 文字目 (1 ≤ p ≤ N) の文字 Cp は E，N，W，S のいずれかである．これらの文字は以下のことを表す．
    • 文字 Cp が E であるならば，p 番目のステップで東隣の交差点に移動することを表す．
    • 文字 Cp が N であるならば，p 番目のステップで北隣の交差点に移動することを表す．
    • 文字 Cp が W であるならば，p 番目のステップで西隣の交差点に移動することを表す．
    • 文字 Cp が S であるならば，p 番目のステップで南隣の交差点に移動することを表す．
    ここで，交差点 (i, j) に対して東隣，北隣，西隣，南隣の交差点はそれぞれ，交差点 (i + 1, j)，交差点 (i, j + 1)，交差点 (i - 1, j)，交差点 (i, j - 1) である．

出力

　標準出力に，ジョイ君の縄張りに属する区画の個数を 1 行で出力せよ．

制限

　すべての入力データは以下の条件を満たす.

  • 1 ≤ N ≤ 100 000．
  • 1 ≤ K ≤ 1 000 000 000．

小課題

小課題 1 [5 点]

　以下の条件を満たす．

  • N ≤ 50．
  • K = 1．

小課題 2 [10 点]

  • K = 1 を満たす．

小課題 3 [23 点]

  • N ≤ 50 を満たす．

小課題 4 [62 点]

　追加の制限はない．

入出力例

入力例 1

12 1
EENWSEEESWWS

出力例 1

3

　この入力例では，散歩は 1 日間で行われる．1 日目にジョイ君は市役所から出発して下図のように移動する．
　黒丸はジョイ君が印を付けた交差点，白丸はジョイ君が印を付けていない交差点，二重丸は市役所のある交差点，数字は各ステップを表す．


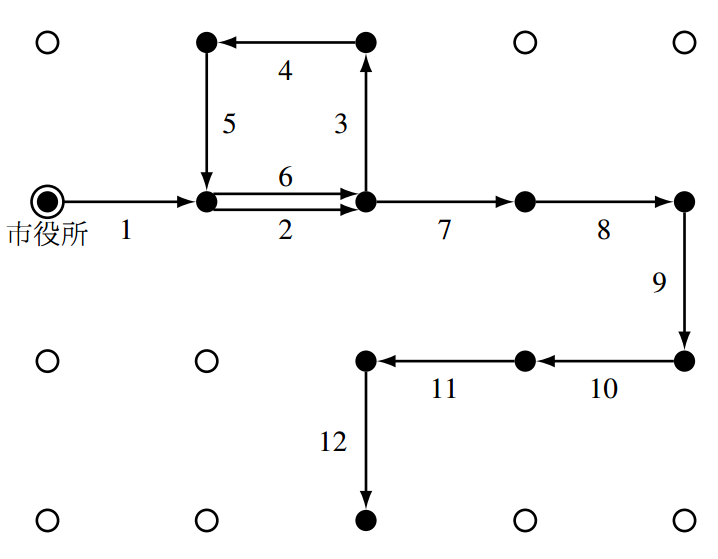
ジョイ君の移動経路

　入力例 1 において，下図の斜線部分で示された 3 個の区画がジョイ君の縄張りに属する．


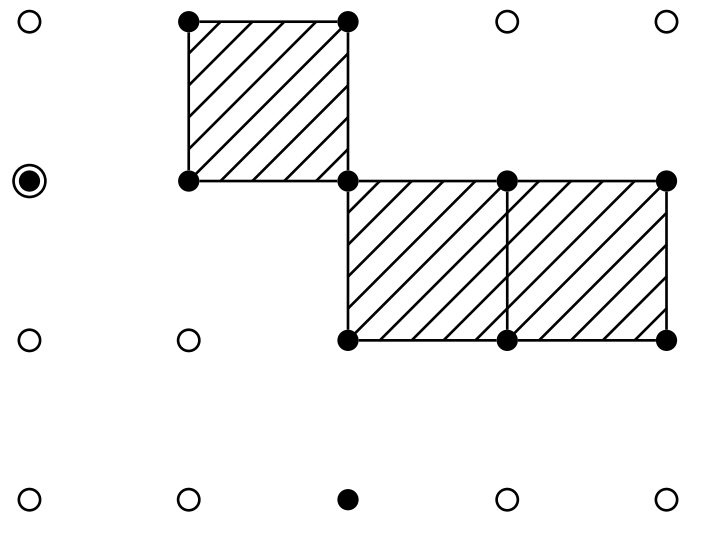
入力例 1 におけるジョイ君の縄張り

入力例 2

12 2
EENWSEEESWWS

出力例 2

7

　入力例 2 では，散歩が 2 日間に渡り行われる．それぞれの日の移動経路は入力例 1 と同一である．散歩が完了したとき，下図の斜線部分で示された 7 個の区画がジョイ君の縄張りに属する．


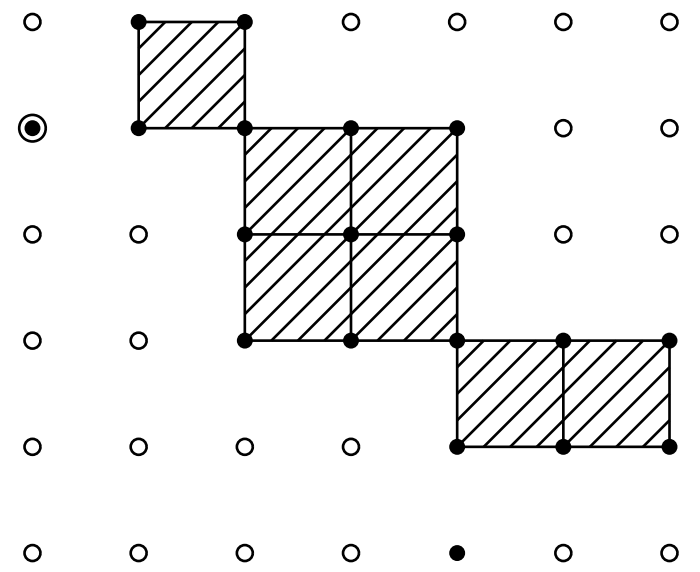
入力例 2 におけるジョイ君の縄張り

　入力例 2 は，小課題 1 および小課題 2 の制約を満たさないことに注意せよ．

入力例 3

7 1
ENNWNNE

出力例 3

0

　入力例 3 では，ジョイ君の縄張りに属する区画は存在しない．

入力例 4

16 5
WSESSSWWWEEENNNW

出力例 4

21

　入力例 4 は，小課題 1 および小課題 2 の制約を満たさないことに注意せよ．