004 - PROBOT
時間制限 1 秒 / メモリ制限 256 MB / 得点 100 / x 1 /
問題
入出力例の画像を見た方がわかりやすいと思います。
縦 $H$ マス、横 $W$ マスの白い盤面がある。
盤面の左から $x$ マス、上から $y$ マスの位置にあるマスを $(x, y)$ と表記する。
左上のマスは $(1,1)$, 右下のマスは $(W, H)$ である。
この盤面の $H \times W$ マスのうち $N$ マスに印を付ける。
印には $1 〜 N$ までの番号が付けられている。$i$ 番目の印は「印 $i$」と呼び、 $(x_i, y_i)$ のマスに位置している。
あなたは以下の性質を持つロボット「PRO-1719」を持っている。
- 印のないマスでは、自分の向いている方向に向かって直進する。
- 印のあるマスでは、自分の向く方向を転換できる。(転換しなくてもよい)
- 向くことのできる方向は、上、下、左、右 の4方向のみである。
- 盤面外へ出てしまった場合は、壊れる。
さて、次のようなとてもおもしろいゲームがある。
- 盤面上のいずれかの印付きマスをスタート地点、それとは別の印付きマスをゴール地点と決める。
- スタートマスに「PRO-1719」を{上,下,左,右}のいずれかの好きな向きで配置して発進させる。
- 印付きマスを適切に経由・適切に方向転換させることを繰り返してゴールマスにたどり着いたらゲームクリア。YTAとじゃんけんできる。
- 盤面外へ出てしまって壊す、またはゴールへたどり着けなくてリタイアした場合は残念賞。YTAから冷凍のお言葉をいただく。
あなたは、スタートマスとゴールマスの選び方によっては絶対にゴールできない場合があることを知った。
$Q$ 回にわたってスタートマスとゴールマスの位置のセットが与えられるので、各セットにおいて、ゲームクリアできるか調べてほしい。
入力形式
H W N x1 y1 x2 y2 : xN yN Q s1 g1 s2 g2 : sQ gQ
1行目に、盤面の縦と横のマス数 $H$, $W$ と 印付きマスの個数 $N$ が入力される。
続く$N$行に、$i$ 番目の印付きマスの座標 $(x_i, y_i)$ が入力される。
次行に、スタート地点とゴール地点のセットの数 $Q$ が入力される。
以下 $Q$ 行、スタートの印付きマスの番号 $s$ と ゴールの印付きマスの番号 $g$ が入力される。
出力形式
各スタート・ゴールのセットについて、適切に方向転換してゴールへたどり着ける場合は "yes", たどり着けない場合は "no" を改行区切りで出力せよ。
制約
- 入力は全て整数である
- $1 \le H,W \le 10^{5}$
- $1 \le N \le 10^{5}$
- $1 \le x_i \le W$
- $1 \le y_i \le H$
- 印のマスの位置は重複しない
- $1 \le Q \le 10^{5}$
- $1 \le s,g \le N$
- $s \neq g$
入出力例
入力例1
3 5 4 2 1 5 3 3 2 2 3 2 1 2 1 3
出力例1
yes no
1つめのセットでは、印 $1$ がスタート、印 $2$ がゴールである。
印 $1$ を下向きで発進して印 $4$ で右向きに方向転換すれば印 $2$ へたどり着ける。
2つ目のセットでは、どうやっても印 $1$ から 印 $3$ へたどり着くことはできない。
ありがたく冷凍のお言葉をいただこう。
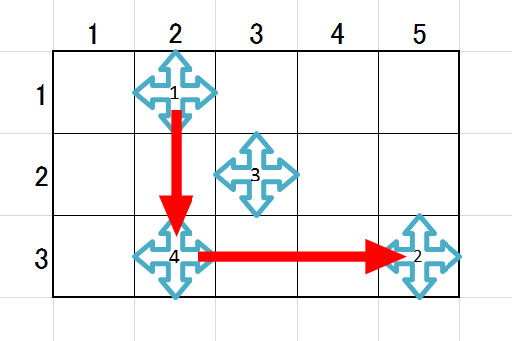
※印の中の数字は、印の番号を表している。
入力例2
100 100 5 2 1 2 8 5 8 5 3 7 3 1 1 5
出力例2
yes
印つきマスを $1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 5$ の順にたどっていけばゴールできる。