002 - 令和の黎明を告げる

問題

あみだくじについて考えます。
まず、N本の水平な縦線をかきます。その線たちは左から線1, 線2, ……, 線Nと名付けます。
その後1からNまでの整数を線の下にかいていきます。ただし範囲内の任意の整数は必ず一度かかれます。言い換えれば1からNまでの整数を並び替えた数列を順番にかくということです。
ここで、線iからあみだくじをスタートして下にたどり着いた時に書かれている数を「線iの解」と呼ぶことにします。
以下のルールに沿ってあみだくじを構築するとき、すべての線iの解がiであるようなあみだくじを作ることができるでしょうか。
できる場合は引く必要のある横棒の最小本数、できない場合はRheinと出力してください。
ルール

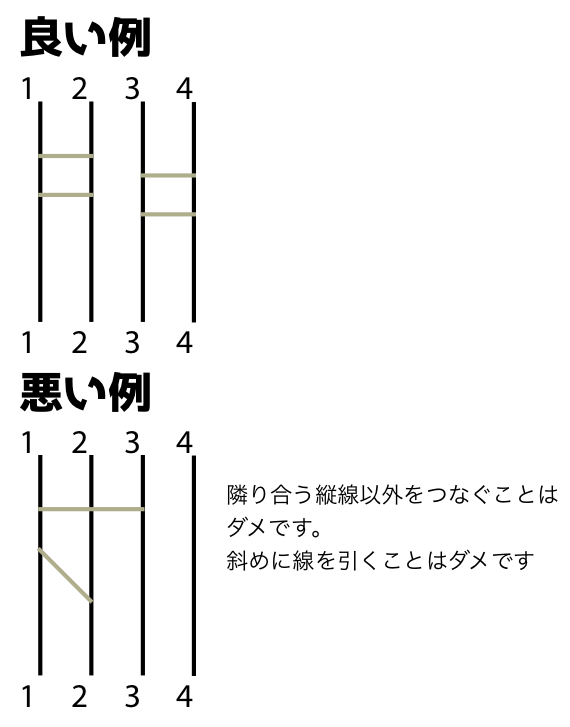
• どの二つの横棒も端点を共有しない
• それぞれの横棒の二つの端点の高さは同じ高さになければならない
• 横棒は隣り合う縦線をつながなければならない

入力

N
線1の下に書かれた数
......
線Nの下に書かれた数

出力

minOrRhein

最小本数またはRheinを出力してください。

制約

テストケース

例1

入力

2
1
2

出力

0

この時線₁の下には1、線₂の下には2が書いてあります。
もともと、全ての線_iの解がiになっているので、横線を引く必要はありません。
よって答えは0となります。

例2

入力

2
2
1

出力

1

この場合、線₁と線₂の間に線を引くと、全ての線_iの解がiにすることができます。
引いた線は1本なので答えは1となります。