011 - 三角形の個数の和

問題

座標平面上の原点$O$を左下、座標$(W,H)$にある点を右上とする長方形の領域が与えられています。この領域に含まれる、$x$座標と$y$座標がともに整数である点を３個以上含む点の集まりを考えます。このような点の集まりのすべての組み合わせの個数を$N$とし、点の集まりのそれぞれを$D_1, D_2, ..., D_N$で表したとき、$D_1, D_2, ..., D_N$のそれぞれに含まれる点を頂点とする三角形を考えます。

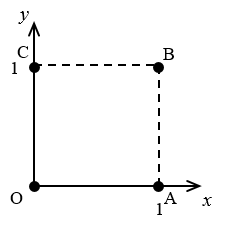
たとえば、図のように$W=H=1$のとき、点$O(0,0)$、$A(1,0)$、$B(1,1)$、$C(0,1)$のうち、３個以上含む点の集まりは$\{O,A,B\}$、$\{O,A,C\}$、$\{O,B,C\}$、$\{A,B,C\}$、$\{O,A,B,C\}$の５つです。この例の場合、点の集まりのそれぞれに含まれる三角形は次のようになります。

• $\{O,A,B\}$に含まれる三角形は$OAB$のみ。
• $\{O,A,C\}$に含まれる三角形は$OAC$のみ。
• $\{O,B,C\}$に含まれる三角形は$OBC$のみ。
• $\{A,B,C\}$に含まれる三角形は$ABC$のみ。
• $\{O,A,B,C\}$に含まれる三角形は$OAB$、$OAC$、$OBC$、$ABC$の４個。

この例からわかるように、同じ三角形が２つ以上の点の集まりに含まれる場合があります。たとえば、三角形$OAB$は点の集まり$\{O,A,B\}$にも$\{O,A,B,C\}$にも含まれます。

$W$と$H$が与えられる。点の集まり$D_1, D_2, ..., D_N$それぞれに含まれる点を頂点とする三角形の個数を$t_1, t_2, ..., t_N$とするとき、三角形の個数の和$t_1+t_2+...+t_N$を計算するプログラムを作成せよ。

入力

入力は以下の形式で与えられる。

$W$ $H$

１行に$W$と$H$ ($1 \leq W,H \leq 1,000$)が与えられる。

出力

それぞれの点の集まりに含まれる三角形の個数の和を1,000,000,007で割った余りを１行に出力する。

入出力例

入力例１

1 1

出力例１

8

入力例２

1 2

出力例２

144

入力例３

100 100

出力例３

879128399