009 - 連環迷路

問題

PCK君は連環迷路で遊んでいる。連環迷路は、座標平面上にある$N$個の円から成り、1つ以上の円の周は原点を通っている。この迷路では、原点をスタート地点として、円の周上だけをたどって移動する。もし、現在たどっている円Aと別の円Bが共有点を持てば、円Aの周上でその共有点まで移動することで円Bの周上に移ることができる。

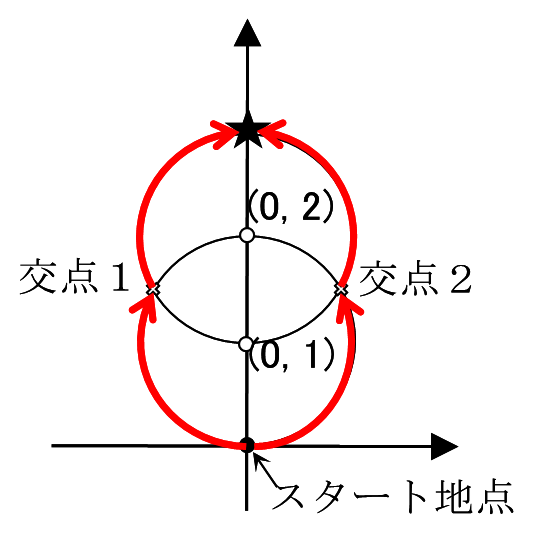
連環迷路のゴール地点は、$N$個の円の周上のうち、スタート地点からの周上に沿った最短の移動距離が最も大きい点である。たとえば、右図のように、中心が(0, 1)にあり半径が1である円Aと、中心が(0, 2)にあり半径が1である円Bがあるとき、スタート地点は円Aの円周上にある。図に示す通り、円Aと円Bの交点は二つある。図中の★印以外で、円周上にあるどの点も、スタート地点からの最短の経路に沿った移動距離は★印よりも近いので、この場合のゴール地点は★印で示した点である。PCK君は、スタート地点からゴール地点までの経路の最短距離を求めたい。

$N$個の円の情報が与えられたとき、スタート地点からゴール地点までの最短距離を求めるプログラムを作成せよ。

入力

入力は以下の形式で与えられる。

$N$
$x_1$ $y_1$ $r_1$
$x_2$ $y_2$ $r_2$
:
$x_N$ $y_N$ $r_N$

１行目に円の数$N$ ($1 \leq N \leq 100$)が与えられる。続く$N$行に、各円の中心のx座標とy座標$x_i,y_i$ ($-10,000 \leq x_i,y_i \leq 10,000$)と半径$r_i$ ($1 \leq r_i \leq 10,000$)が、整数で与えられる。ただし、中心の座標と半径が同じ円は与えられない($i \ne j$なら、$x_i \ne x_j$ または$y_i \ne y_j$ または$r_i \ne r_j$)。スタート地点がある円から、いくつかの円をたどることで、どの円の周上にも到達できる。また、円同士が共有点を持たない場合、それら２つの円の周上の最近接点同士は、0.0001以上離れているとする。

出力

最短距離を実数で１行に出力する。ただし、誤差がプラスマイナス 0.0001を超えてはならない。この条件を満たせば小数点以下は何桁表示してもよい。

入出力例

入力例１

2
1 0 1
3 0 1

出力例１

6.28318531

入力例２

4
1 0 1
3 0 1
2 2 1
4 2 2

出力例２

10.35207318

入力例３

2
0 1 1
0 2 1

出力例３

4.1887902