012 - 三角形パズル

問題

平面上に２つ以上の三角形の集合が与えられる。与えられる三角形は、以下の条件を満たすものとする。

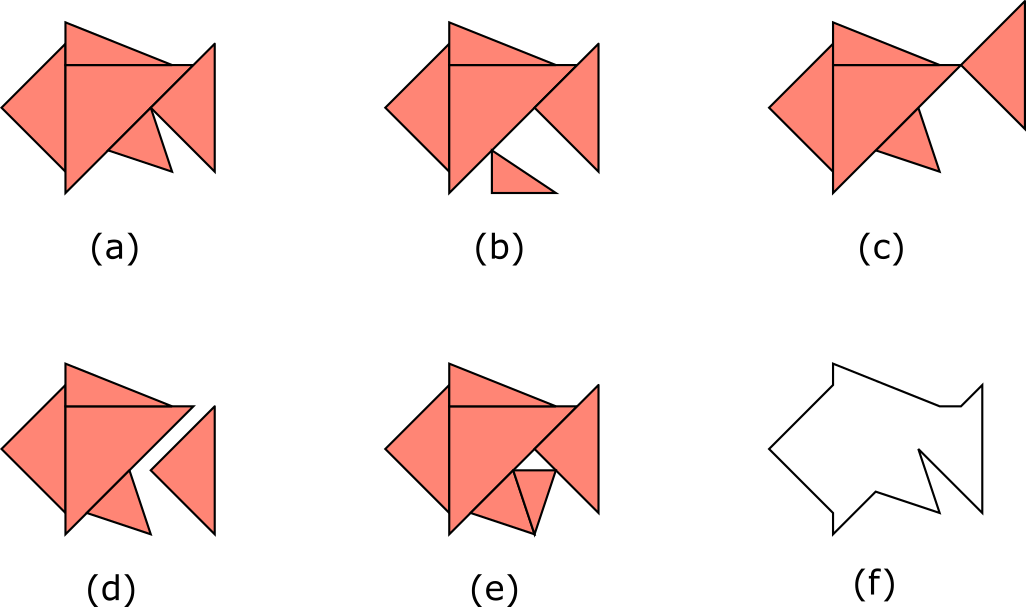
• これらの三角形が互いに重なることはない。
• 各三角形は、少なくとも他の一つの三角形と、辺の一部を共有して連結している。ただし、２つの三角形が１点だけを共有する場合は、連結とはみなさない。つまり、図(b)、図(c)、図(d)のような三角形の集合は与えられない。

三角形の集合が形成する多角形の内部は、三角形によりすべて埋め尽くされている。つまり、図(e)のような三角形の集合は与えられない。

これらの三角形で形成される多角形のすべての頂点の座標を求めよ。たとえば、図(a)の三角形の集合からは、図(f) の多角形が得られる。

上の条件を満たすように２つ以上の三角形が与えられたとき、それらが形成する多角形のすべての頂点の座標を求めるプログラムを作成せよ。

入力

入力は以下の形式で与えられる。

$N$
$Triangle_1$
$Triangle_2$
:
Triangle_N$

１行目に、三角形の個数$N$ ($2 \leq N \leq 100,000$)が与えられる。 続く$N$行に、$i$番目の三角形の情報$Triangle_i$が与えられる。各$Triangle_i$は以下の形式で与えられる。

$x_1$ $y_1$ $x_2$ $y_2$ $x_3$ $y_3$

$i$番目の三角形のj番目の頂点の$x$座標$x_j$ ($-1,000,000,000 \leq x_j \leq 1,000,000,000$)と$y$座標$y_j$ ($-1,000,000,000 \leq y_j \leq 1,000,000,000$)が、それぞれ整数で反時計回りの順に与えられる。

出力

三角形の集合が形成する多角形の輪郭線に沿って、多角形の各頂点のx座標とy座標を表す整数の組を、空白区切りで１行に出力する。頂点は以下の順番で出力する。

• 起点となる頂点P1を出力する。起点とはy座標が最も小さい頂点である。そのような頂点が複数ある場合は、それらの中でx座標が最も小さい頂点を起点とする。
• ２番目の点を出力する。２番目の点は、P1を中心としてx軸の正の方向を基準として反時計回りに見たとき最初に見つかるP1と直接つながる頂点とする。
• ３番目以降は、直前に出力した点と直接つながる頂点のうち、未訪問の点を出力する。

入出力例

入力例１

2
0 0 4 4 0 4
1 1 3 1 3 3

出力例１

0 0
1 1
3 1
3 3
4 4
0 4

入力例２

3
0 0 2 0 1 2
2 0 3 2 1 2
2 0 4 0 3 2

出力例２

0 0
4 0
3 2
1 2

下図の(a)(b)はそれぞれ入力例２と出力例２を表す。