006 - 一筆書き

問題

PCK君が画用紙に絵を描いている。PCK君は以下のように絵を描く。

• 一回の動作で、１つの線分を描く。
• 既に描かれている線分に触れる場合は、お互いの端点だけで重なる。

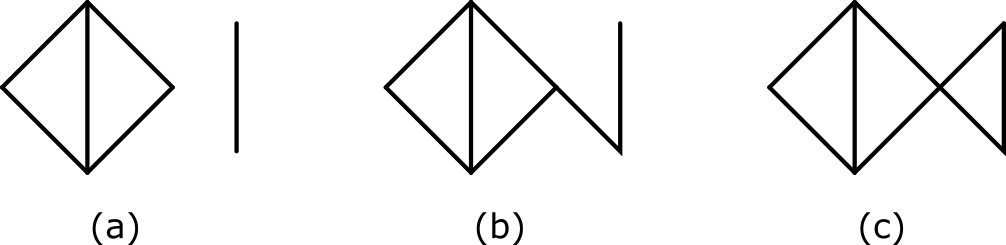
この動作を繰り返すと、画用紙にはいくつかの図形が現れる。ここでは、連結した線分のグループを１つの図形とする。たとえば、図(a)には、それぞれ５本と１本の線分からなる２つの図形が描かれている。図(a)に1本の線分を追加して図(b)のように描くと、７本の線分からなる１つの図形になる。

画用紙に描かれている図形の中で、一筆書きが可能なものはいくつあるだろうか？一筆書きとは、筆記具を画用紙から一度も離さず、同じ線を二度なぞらずに線図形を描くことである。ただし、同じ端点を何回通っても構わない。たとえば、図の(a)、(b)、(c)の順に描いていったとき、それぞれで一筆書きが可能な図形は、２個、０個、１個ある。

PCK君が線分を描く動作の情報が順番に与えられる。動作が終わるごとに、画用紙に含まれる一筆書きが可能な図形の数を報告するプログラムを作成せよ。

入力

入力は以下の形式で与えられる。

$N$
$segment_1$
$segment_2$
:
$segment_N$

１行目に、線分の数$N$ ($1 \leq N \leq 200,000$)が与えられる。続く$N$行に、$i$番目の動作で描く線分の情報が与えられる。ただし、同じ線分が与えられることはない。各線分は以下の形式で与えられる。

$x_1$ $y_1$ $x_2$ $y_2$

線分の始点の座標$x_1$, $y_1$ ($0 \leq x_1,y_1 \leq 1,000,000,000$)と終点の座標$x_2$, $y_2$ ($0 \leq x_2, y_2 \leq 1,000,000,000$)が整数で与えられる。ただし、始点と終点の座標が同じものが与えられることはない（$x_1 \ne x_2$ または $y_1 \ne y_2$）。

出力

各動作の後に、一筆書きが可能な図形の個数を１行に出力する。

入出力例

入力例

8
5 0 8 3
5 6 2 3
10 5 10 1
2 3 5 0
5 0 5 6
8 3 5 6
8 3 10 1
10 5 8 3

出力例

1
2
3
2
2
2
0
1