002 - PRO製造機

時間制限 1 秒 / メモリ制限 32 MB / 得点 100 / x 6 /

TLE
1sec
MLE
32MB
得点
100

もんだい

あるH工場では、"PRO"を製造しています。
倒産してしまいそうなこの工場は"PRO"を効率よく生産することが大切です。
なので、効率よく生産するために、"PRO"を作る材料を計画的に揃えることにしました。
この工場では、最終的に製造する"PRO"を製品番号 N とし、製品番号 1 〜 N-1 の材料となる製品を取り扱っています。

1〜N-1 の製品は購入するか、この工場で製造するかのどちらかにより入手することにしています。
この工場はプライドが高いせいか、あまり製品を購入することは好きではありません。
なので"PRO"である製品 N も含めて、製造できる製品は購入せずに、必ず製造することにしています。

しょうさい

入力に各製品の製造方法が与えられるので、"PRO"である製品 N を1個作るために、購入する必要のある最小の個数を1〜N-1番の製品ごとにそれぞれ1行で出力してください。


製品iの製造方法が複数与えられた場合は、それらすべての材料を必要とします。
また、製品Nを製造するための製造方法は必ず与えられるとします。

にゅうりょく

N
M
P1 Q1 R1
P2 Q2 R2
   :
PM QM RM

1行目に、製品の個数 N (2 ≦ N ≦ 100) が与えられる。
2行目に、製造方法の数 M (1 ≦ M ≦ 350) が与えられる。
3行目からM+2行目までに、製造方法を表す3つの整数が空白区切りで与えられる。
Pi : 材料の製品番号 (1 ≦ Pi ≦ N)
Qi : 材料の個数 (1 ≦ Qi ≦ 100)
Ri : 製造する製品番号 (1 ≦ Ri ≦ N)

しゅつりょく

製造番号1の購入数 (S1)
製造番号2の購入数 (S2)
:
製造番号iの購入数 (Si)
:
製造番号N-1の購入数 (SN-1)

Si は "232-1" (4294967295) を超えることはない。

さんぷる

入力例1

2
1
1 5 2

出力例1

5

解説

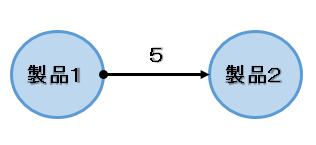
"PRO"(製品２)を作るためには製品１が５個必要である。
製品１を製造する方法がないため、製品１を５個買うことになる。

入力例2

4
3
1 1 2
2 3 4
3 1 4

出力例2

3
0
1

解説

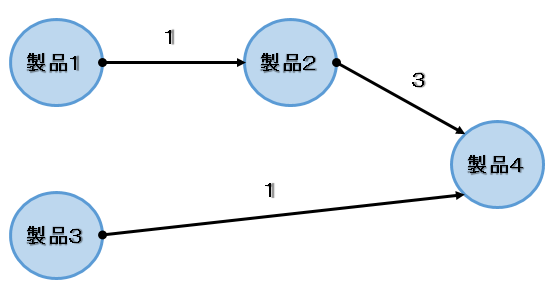
"PRO"(製品４)を作るためには製品２が３個と、製品３が１個必要である。
製品２は製品１を１個使って製造できるので、製品１を３個買って製品２を３個作る。
製品３は製造する方法がないため、製品３を１個買うことになる。

入力例3

9
10
1 11 2
7 12 8
8 13 1
2 14 9
8 15 9
8 16 4
3 17 4
4 18 5
5 19 9
2 20 4

出力例3

0
0
5814
0
0
0
11827308
0