003 - ケーキカット

本日，世界有数のケーキ職人として知られる Bon Vivant 氏が誕生日を迎える． 誕生日パーティには世界中から美食家達が招かれ，みんなが Vivant 氏の独創性あふれるケーキを待ちわびている． ちょうど今，パーティ会場に大きな四角いケーキが運び込まれてきた． 美しいデコレーションもなく素朴に見えるが，想像を絶するくらいおいしいに違いない． このケーキを，ナイフで複数のピースにカットし，パーティの参加者にふるまいたい．

ケーキを真上から見ると長方形に見える(図 C-1)． 図 C-2 に例示したように，十分な数のピースが得られるまで，ケーキのカットが繰り返し行われる． 1回のカットでは，ちょうど一つのピースを二つのより小さなピースに切り分ける． ナイフの切り口は，必ず，底面とは垂直，側面とは水平または垂直になるようにする． したがって，すべてのピースは上から見ると長方形で，側面は垂直になる．

図 C-1: 真上から見たケーキ

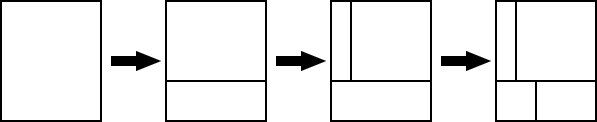
図 C-2: ケーキの切り分け

図 C-2 では，ピースのサイズがまちまちで不公平に見えるかもしれないが，気にすることはない． なるべく多くの種類のケーキを食べたい招待客は，小さなピースを好むことが多い． もちろん，大きなピースを好む者もいる．

この問題では，ケーキをカットする過程をシミュレートし，各ピースのサイズを出力するプログラムを作って欲しい．

入力はデータセットの列であり，各データセットは次のような形式である．

n  w  d
p₁  s₁
...
p_n  s_n

最初の行の n は，0 以上 100 以下の整数であり，カットの回数を表す． 同じ行の w と d は，1 以上 100 以下の整数であり，それぞれケーキの幅と奥行きを表す． 以下では，東西方向の長さが w，南北方向の長さが d となるようにケーキが置かれているものとする．

続く n 行でカットの方法を指定する． 1回のカットでは，ちょうど1個のピースのみを2分割する． p_i は i 回目にカットするピースの識別番号で，1 以上 i 以下の整数である． i 回目のカットを行う直前には，ちょうど i 個のピースが存在し， それぞれに 1, 2, ..., i の識別番号が，以下の条件を満たすように与えられる．

• 先に生まれたピースほど識別番号が小さい．
• 1回のカットで生まれる二つのピースについては，（上から見た）面積の小さい方が識別番号も小さい． 二つのピースの面積が同じになる場合には，どちらの識別番号が小さいと考えても構わない（どちらにしても最終的な答えには影響しない）．

なお，この識別番号は，1回カットが行われるたびに付け替えられる．

s_i は，1 以上 1000 以下の整数で，i 回目のカットの起点を表す． カットすべきピースの周囲を，北西の角から時計回りに s_i 進んだ地点がカットの起点になる． なお，こうやって決められた起点が，ピースの四隅の角のうちのどこかと一致することはない． この起点から，（この起点を含む）側面と垂直にピースのカットは行われる．

入力の終わりは，三つのゼロを含む行で示される．

各データセットに対し，指定された n 回のカットがすべて終了した段階で存在する全ピースの上から見た面積を小さい方から順番に列挙し，空白文字１個のみを区切り記号として１行に出力せよ． 同じ面積のピースが複数存在する場合には，ピースの個数分だけ重複して面積の出力を行うこと．

3 5 6
1 18
2 19
1 2
3 4 1
1 1
2 1
3 1
0 2 5
0 0 0

4 4 6 16
1 1 1 1
10