002 - 舞踏会 (Ball)

問題

　IOI 王国では，王女である JOI 姫の誕生日を祝って舞踏会が開かれることになった．
　舞踏会には N 人の貴族が参加する予定である．N は奇数である．貴族には 1 から N までの番号が付けられている．それぞれの貴族には踊りのうまさという整数が定められており，貴族 i (1 ≤ i ≤ N) の踊りのうまさは D_i である．
　舞踏会では JOI 姫を含む N + 1 人で 2 人ずつ組を作って踊る．IOI 王国では，上級者が初級者を補助できるように，伝統的に以下の方法で踊りの組を決定している．

• 最初に，N 人の貴族が 1 列に並ぶ．
• 列に並んでいる貴族が 1 人になるまで，以下の操作を繰り返す．
• 列の先頭から 3 人の貴族の踊りのうまさを調べる．
• その 3 人の貴族の中で，最も踊りのうまさが大きい貴族を A とおく．ただし，複数いる場合は，最も踊りのうまさが大きい貴族の中で，最も番号の小さい貴族 を A とおく．
• その 3 人の貴族の中で，最も踊りのうまさが小さい貴族を B とおく．ただし，複数いる場合は，最も踊りのうまさが小さい貴族の中で，最も番号の大きい貴族 を B とおく．
• A と B が列から抜けて組になる．
• 残った 1 人は列の最後尾に移動する．
• 最終的に残った 1 人が JOI 姫と組になる．

　貴族 1 から貴族 M (1 ≤ M ≤ N - 2) の M 人の貴族については，すでに初期状態で列の何番目に並ぶのかが決まっている．残りの N - M 人の貴族の並び方は国王が自由に決めることができる．
　JOI 姫は踊りを学んだばかりなので，国王は JOI 姫と組になる貴族の踊りのうまさをできるだけ大きくしたいと考えている．JOI 姫と組になる貴族の踊りのうまさとして考えられる最大値を求めよ．

課題

　それぞれの貴族の踊りのうまさと，M 人の貴族の初期状態で並ぶ場所が与えられたとき，JOI 姫と組になる貴族の踊りのうまさとして考えられる最大値を求めるプログラムを作成せよ．

入力

　標準入力から以下のデータを読み込め．

• 1 行目には，2 個の整数 N, M が空白を区切りとして書かれている．これは舞踏会に貴族が N 人参加し，列に並ぶ場所がすでに決まっている貴族が M 人いることを表す．
• 続く M 行のうちの i 行目 (1 ≤ i ≤ M) には，2 個の整数 D_i, P_i が空白を区切りとして書かれている．これは貴族 i の踊りのうまさが D_i で，貴族 i が初期状態で列の先頭から P_i 番目に並ぶことを表す．
• 続く N - M 行のうちの i 行目 (1 ≤ i ≤ N - M) には，整数 D_i+M が書かれている．これは貴族 (i + M) の踊りのうまさが D_i+M であることを表す．

出力

　標準出力に，JOI 姫と組になる貴族の踊りのうまさとして考えられる最大値を表す整数を 1 行で出力せよ．

制限

　すべての入力データは以下の条件を満たす．

• 3 ≤ N ≤ 99 999．
• N は奇数である．
• 1 ≤ M ≤ N - 2．
• 1 ≤ D_i ≤ 1 000 000 000 (1 ≤ i ≤ N)．
• 1 ≤ P_i ≤ N (1 ≤ i ≤ M)．
• P_i ≠ P_j (1 ≤ i < j ≤ M)．

小課題

小課題 1 [8 点]

• N ≤ 9 を満たす．

小課題 2 [16 点]

• N ≤ 19 を満たす．

小課題 3 [44 点]

• N ≤ 1 999 を満たす．

小課題 4 [32 点]

　追加の制限はない．

入出力例

入力例 1

7 3
5 2
5 5
8 6
6
2
8
9

出力例 1

8

　初期状態では 3 人の貴族の並ぶ場所がすでに決まっている．

括弧内の数字は踊りのうまさを表す．左端が列の先頭である．

　例えば，先頭から順に貴族 5，貴族 1，貴族 4，貴族 6，貴族 2，貴族 3，貴族 7 という順番に並んだ場合を考える．

すべての貴族が並んだあとの配置

　この場合，以下のように列が変化していく．

• 列の先頭の 3 人の貴族 (貴族 5，貴族 1，貴族 4) 中で，最も踊りのうまさが大きい貴族 4 と最も踊りのうまさが小さい貴族 5 が組になり，残った貴族 1 が最後尾に移動する．
• 次に，列の先頭の 3 人の貴族 (貴族 6，貴族 2，貴族 3) の中で，最も踊りのうまさが大きい貴族は貴族 6 と貴族 3 の 2 人であり，このうち番号の小さい貴族は貴族 3 である．また，列の先頭の 3 人の貴族のうち最も踊りのうまさが小さい貴族は貴族 2 である．貴族 3 と貴族 2 が組になり，残った貴族 6 が最後尾に移動する．
• 次に，列の先頭の 3 人の貴族 (貴族 7，貴族 1，貴族 6) の中で，最も踊りのうまさが大きい貴族 7 と最も踊りのうまさが小さい貴族 1 が組になり，残った貴族 6 が最後尾に移動する．
• 最終的に貴族 6 が残り，JOI 姫と組になる．

　貴族 6 の踊りのうまさは 8 である．この値が JOI 姫と組になる貴族の踊りのうまさとして考えられる最大値である．

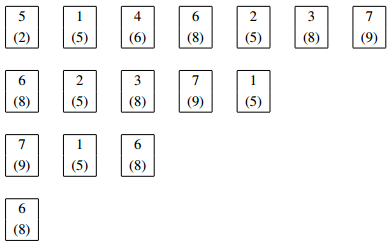
列の変化の様子

入力例 2

3 1
5 3
5
5

出力例 2

5

　どのような順番で並んでも，貴族 2 と JOI 姫が組になる．

入力例 3

7 2
32 4
27 6
37
41
41
30
27

出力例 3

37