問題文
神話歴1710年、この世は世界蛇に食べ尽くされてしまった。
ゴッド・ナカムーは怒った。「蛇の頭を一突きに仕留めてくれようぞ。」
蛇の尾の先端の位置$(sx, sy)$と蛇の全長nメートル、また蛇が上向きにまっすぐ横たわっていることが分かっている。
この後、蛇はQ回にわたって体を曲げる。体を曲げる位置は、尾の先端から$t_i$メートルの場所であり、曲げた方向は$d_i$である。
Q回の行動毎に頭の位置を出力せよ。
入力
n q sx sy t1 d1 t2 d2 .. tq dq
制約
すべてのテストケースにおいて以下を満たす
- $1 \le n \le 10^5$
- $1 \le q \le 10^5$
- $-10^9 \le sx \le 10^9$
- $-10^9 \le sy \le 10^9$
- $1 \le t_i \le n - 1$
$n, q, sx, sy, t_i$はすべて整数である。
$d_i$ は 'L', 'R' のいずれかであり、
$d_i$が'L'のとき蛇の進行方向に対して左に、'R'のとき蛇の進行方向に対して右に体を曲げたことを表す。
つまり、$d_i$が'L'のとき$t_i$までの体と$t_i$より先の体が成す角は、時計回りに270度、
$d_i$が'R'のとき$t_i$までの体と$t_i$より先の体が成す角は、時計回りに90度になる。
出力
$Q$回の行動毎に頭の位置を改行区切りで出力せよ
入出力例
入力
5 3 0 0 4 L 2 R 3 L
出力
-1 4 2 3 0 3
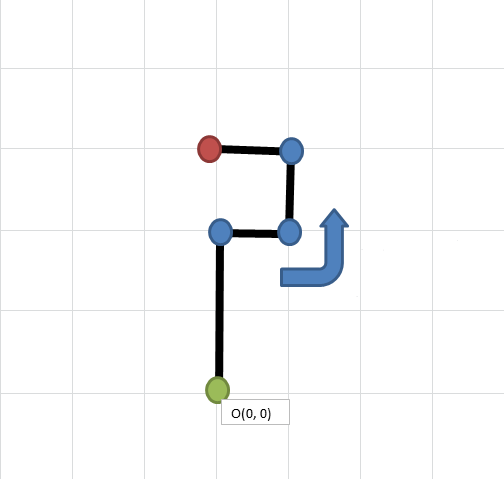
蛇は次のように動く
赤の丸が蛇の頭、緑の丸が尾の先端を示す。
1回目の行動直後
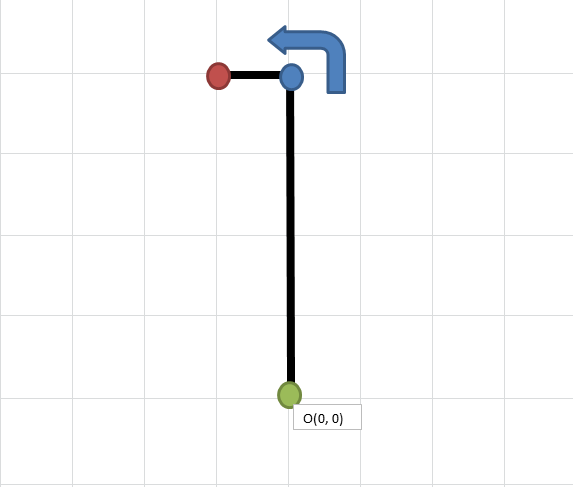
2回目の行動直後
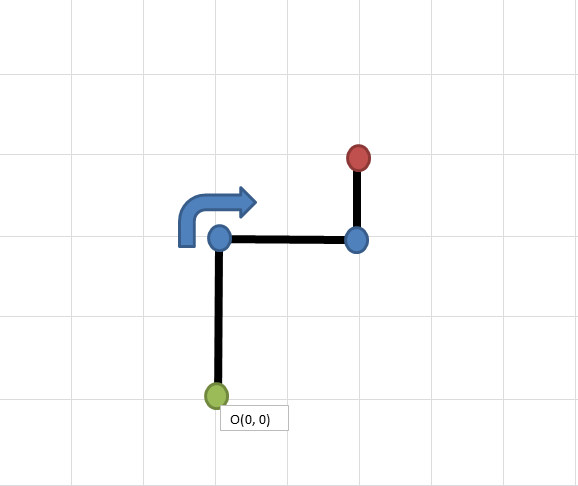
3回目の行動直後