ストーリー
古代遺跡から不思議な装置が発見された。発見された装置は、両面に整数が書かれた円盤、整数が書かれたカードの束、カードの束を入れる台からなる。台にカードの束を入れると、円盤が回転する。円盤は、常に片面だけが見えている。
円盤は中心から角度が均等になるようにK個の区画に分割されていて、表側に $1$ から $K$ までの整数が順番に時計回りに刻まれている。また、円盤は裏表で区画の境界を共有しており、ある区画の表側に数 $X$が刻まれているとき、その裏側には数-$X$ が刻まれている。されに、円盤の外側には針が存在し、ある一つの区画の弧の中心を指し示している。以降、見えている面の針が指し示している値が $X$ であるとき、円盤は $X$ にセットされていると呼ぶ。
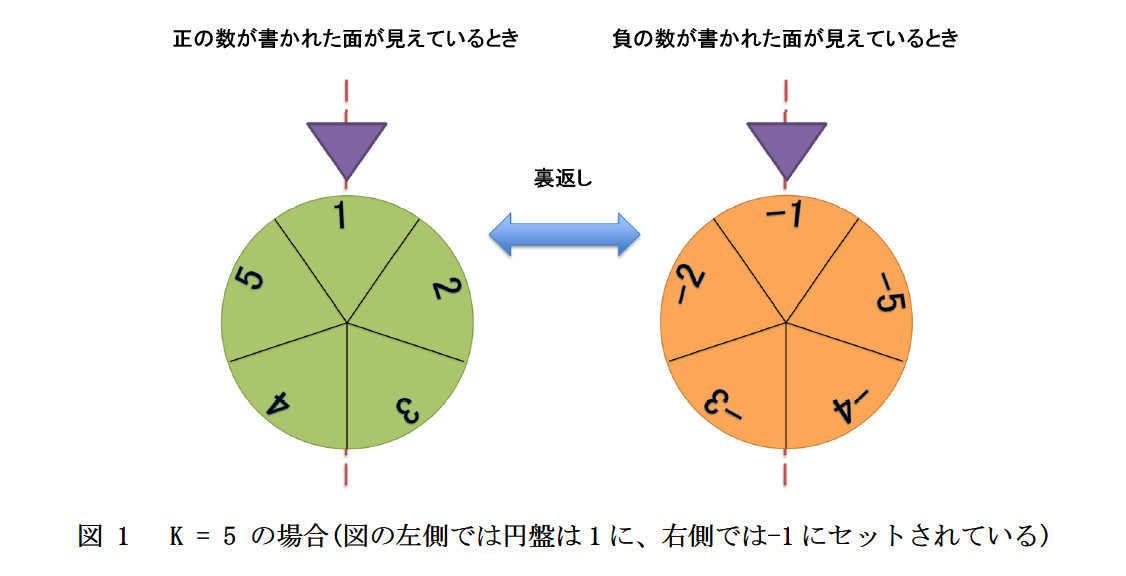
調査の結果、装置の挙動について以下のことが判明した。
装置の台にカードの束を入れると、装置は円盤を 1 にセットする。
その後、装置はカードを上から順に読み込んでいき、書かれている数$A$に応じて以下のように動作する。
- Aが正の数の時 円盤を図の時計回りに|$A$|区画を回転させる
- Aが0の時 針と円盤の中心を通る直線を軸として、円盤を裏返す
- Aが負の数の時 円盤を図の反時計回りに|$A$|区画を回転させる
装置の情報と命令がかかれたカードの束の内容が与えられたとき、各命令後に針が指し示している値を記録するのがあなたの役目である。
入力
1行目に、区間の個数$K$、カードの枚数$N$が与えられる。2行目以降N行に渡ってカードに書かれている整数が与えられる。
K N A0 A1 ... AN
出力
各命令後に装置にセットされている値を一行ずつN個出力せよ。最後の改行を忘れずに。
制約
- 2 ≤ $K$ ≤ 108
- 1 ≤ $N$ ≤ 105
- 0 ≤ |$A$i| ≤ 109
入出力例
例1
入力
5 3 1 0 -2
出力
5 -5 -3
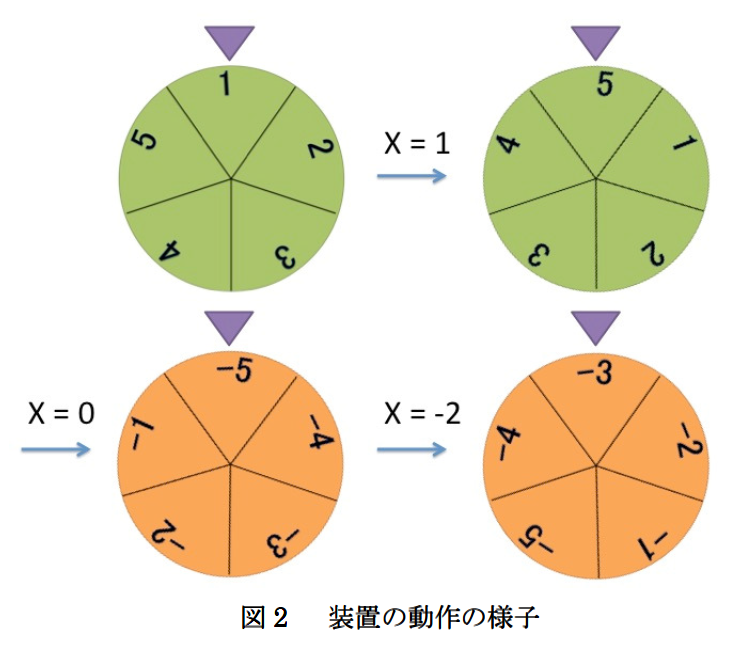
各命令後はこういう動きをする。
例2
入力
10 4 100 -1 0 -1000
出力
1 2 -2 -2