問題
とある建設会社が南北方向に一直線上に並んだ$ \ N \ $個の区画に新たにマンションを建設しようと考えている。
しかし、$N \ $個の区画のうち$ \ M \ $個の区画には既にマンションが存在するためその区画に新たにマンションを建設することは出来ない。
$p_i \ $番目の区画には高さ$ \ h_i \ $のマンションが存在する。
建設会社は既に存在するマンションを含め全てのマンションに太陽光が当たるようにしたいため、$i \lt j \ $のとき$ \ i \ $番目のマンションの高さは $ \ j \ $番目のマンションの高さよりも高くしなければならない。
しかし、建設会社は技術力に限界があるため高さ$ \ H \ $以下のマンションしか建設出来ない。
建設会社が$ \ N \ $個の区画に高さの総和が出来るだけ大きくなるように新たなマンションを建設する時、新たに建設したマンションの高さの総和を求めなさい。
※$ \ 1 \ $つの区画には$ \ 1 \ $つのマンションしか存在することはできない。
※高さ$ \ 0 \ $はその区画にマンションが存在しないことを表す。
入力
$N \ M \ H$ $p_1 \ h_1$ $p_2 \ h_2$ $\vdots$ $p_M \ h_M$
出力
高さの総和を$ \ 1 \ $行で出力せよ。出力の末尾には改行を入れること。
制約
- $2 \leq N \leq 10^6$
- $0 \leq M \leq N$
- $1 \leq H \leq 10^9$
- $1 \leq p_i \leq N$
- $1 \leq h_i \leq H$
- $p_i \lt p_j \ (i \lt j)$
- $h_i \gt h_j \ (i \lt j)$
- $1 \ $つの区画に複数のマンションが存在するような入力は与えられない
入出力例
例1
入力
5 1 7 3 4
出力
18
解説
高さは$ \ 7,6,4,3,2 \ $となり、$7+6+3+2 = 18 \ $となる。
下図(黒 : 既に存在するマンション 青 : 新たに建設するマンション)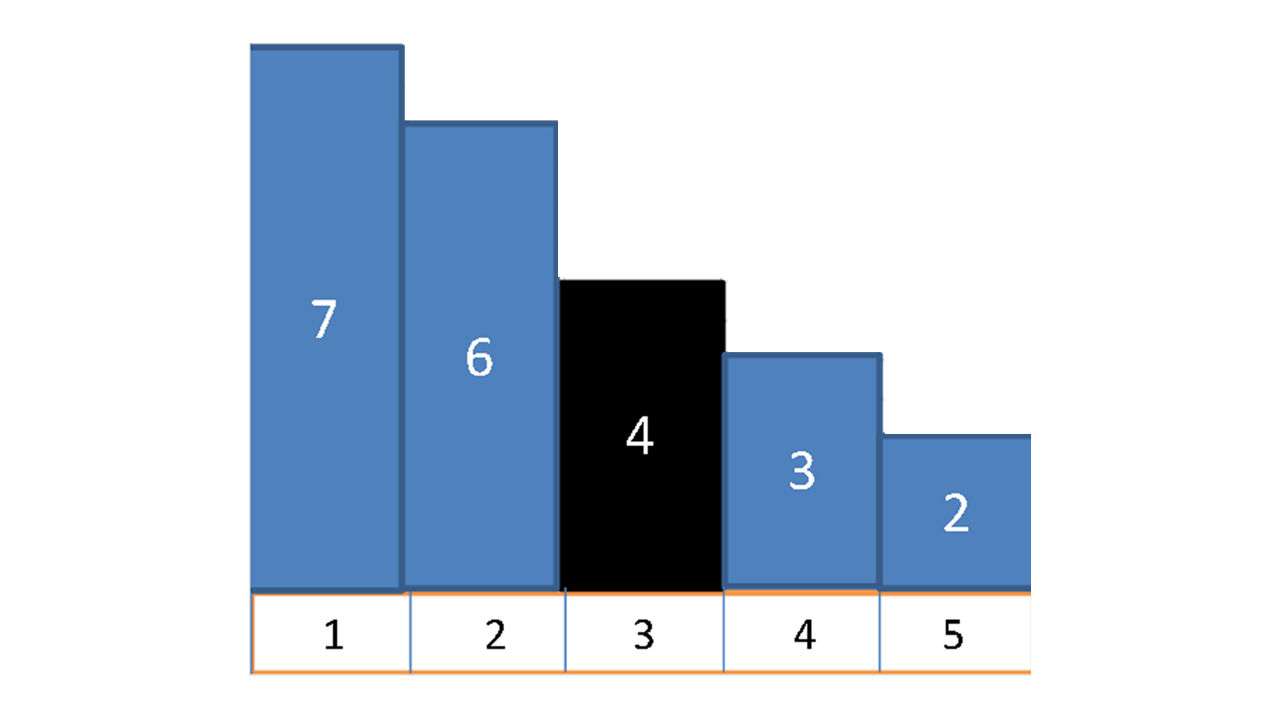
例2
入力
4 4 6 1 5 2 4 3 3 4 2
出力
0
解説
高さは$ \ 5,4,3,2 \ $となり、全ての区画にマンションが建設されているため新たに建設することができないので$ \ 0 \ $と出力する。
下図(黒 : 既に存在するマンション 青 : 新たに建設するマンション)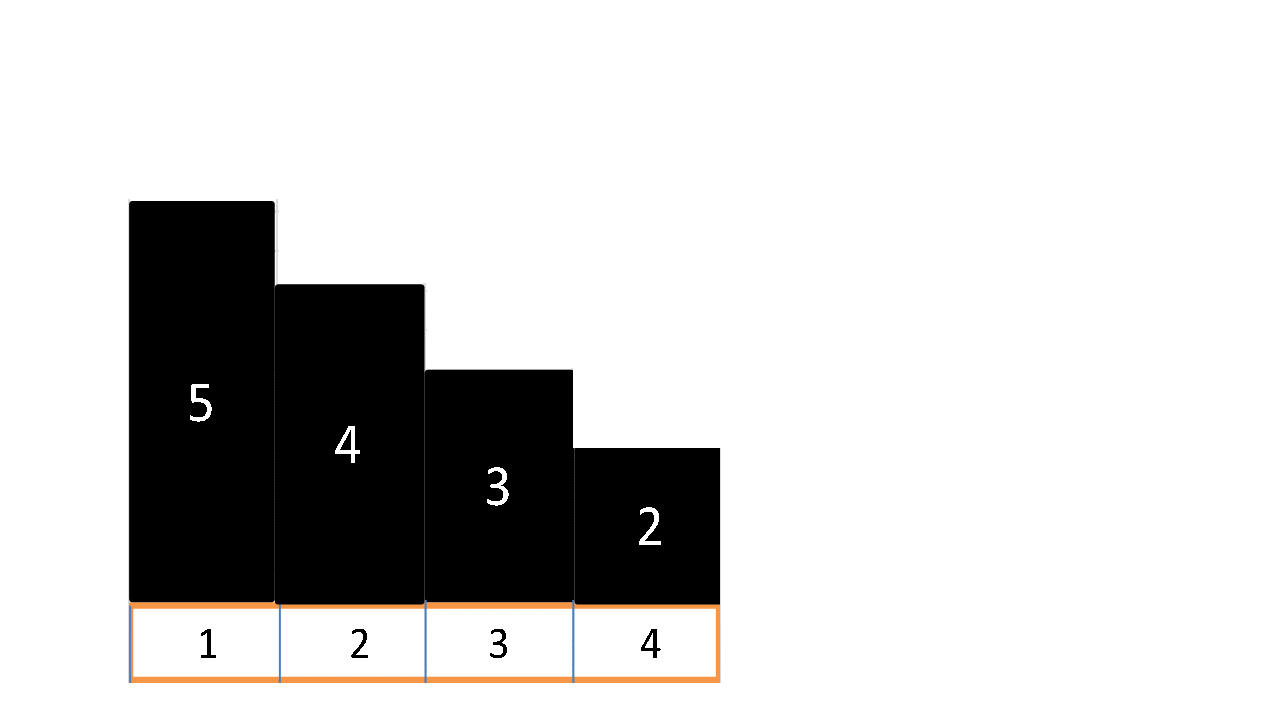
例3
入力
6 2 8 2 5 5 3
出力
14
解説
高さは$ \ 8,5,0,4,3,2 \ $もしくは$ \ 8,5,4,0,3,2 \ $となり、$8+4+2 = 14 \ $となる。
下図(黒 : 既に存在するマンション 青 : 新たに建設するマンション)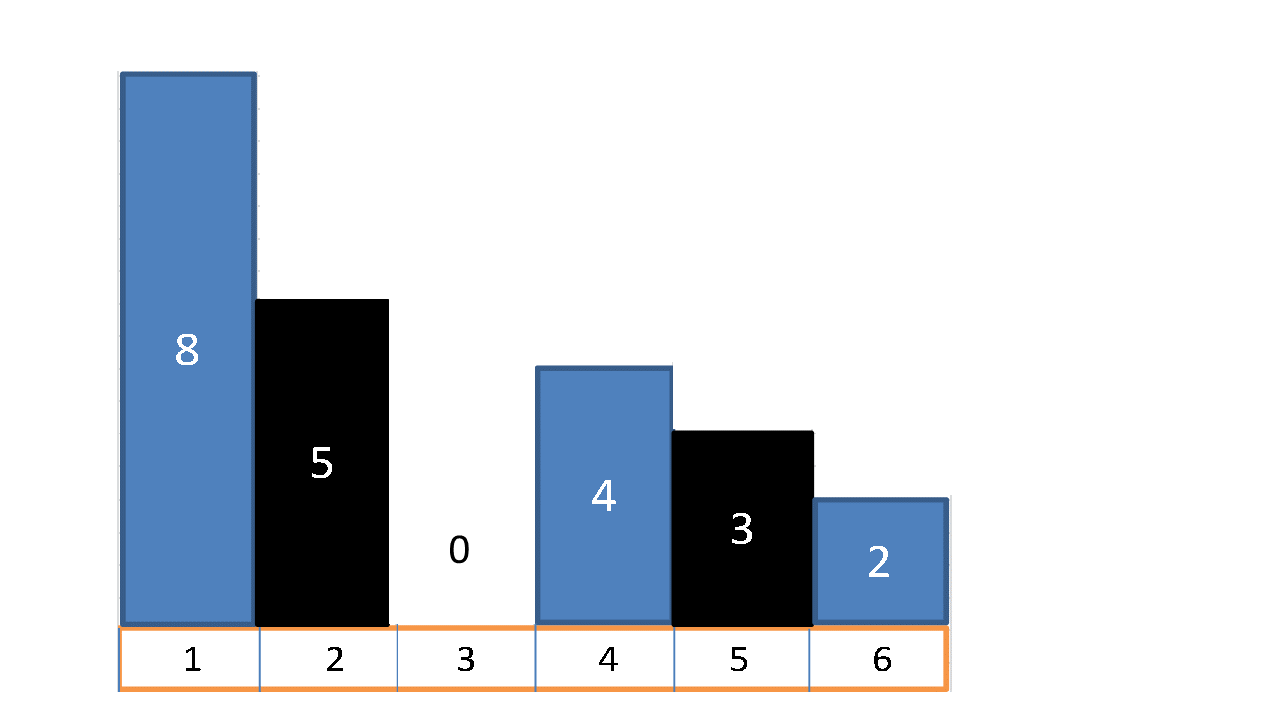
例4
入力
6 2 8 1 8 3 7
出力
15