1228 - Chocolate

問題

縦 H ピース、横 W ピースでできた一枚のチョコレートがある。(ピースは全て同じ大きさの正方形)
あなたはこのチョコレートを何回か切って N ピースでできた一枚のチョコレートにしたいと考えている。
何回切ることで N ピースでできた一枚のチョコレートにすることができるだろうか。切る最小の回数を出力せよ。
ただし、切る際には以下のルールがある。

• 切るときにはピースの境目に沿って縦一直線、又は横一直線にしか切ることは出来ない。
• 一回も切らなくてもよい。
• 切り終わった N ピースでできたチョコレートは長方形でなくてはいけない。

入力

H W N

出力

最小で何回切ることで条件を満たすチョコレートにすることができるか出力せよ。
また、何回切っても条件を満たすチョコレートにすることができない場合は-1と出力せよ。
出力の末尾には改行を入れること。

制約

• 1 ≤ H,W ≤ 10⁶
• 1 ≤ N ≤ 10¹²

小課題

1.(30点)

• 1 ≤ H,W ≤ 10³
• 1 ≤ N ≤ 10⁶

2.(70点) 追加の制約はない。

入出力例

例１

入力

2 4 3

出力

2

解説
1回目:縦,2回目:横と、以下のように赤い線で切ればよい。

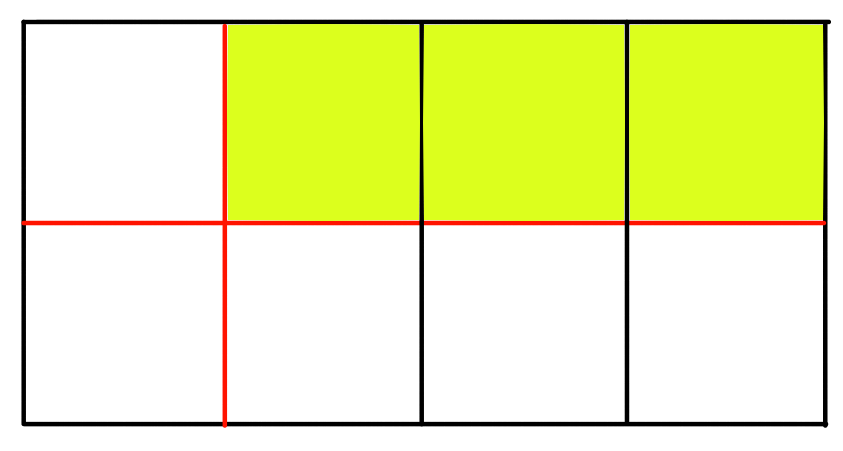
例２

入力

2 3 5

出力

-1

例３

入力

3 3 9

出力

0