問題
自称数学者の山本君は正多角形が大好きです。
山本君は山田君から面積が$1$の正三角形を $N$ 個貰いました。
しかし、山本君は面積の大きい正多角形の方が好きなので $N$ 個の正三角形のうちいくつかを組み合わせて、できるだけ面積の大きい正多角形を作ることにしました。
山本君の作ることのできる正多角形の最大の面積を出力してください。
また、正多角形を作る際は以下の条件をすべて満たすこと。
- 組み合わせる正三角形は互いに辺を共有する。
- 正多角形の内部は正三角形によって隙間なく敷き詰められている。
- 正三角形は重ねてはならない。
条件を満たす例
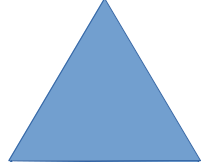
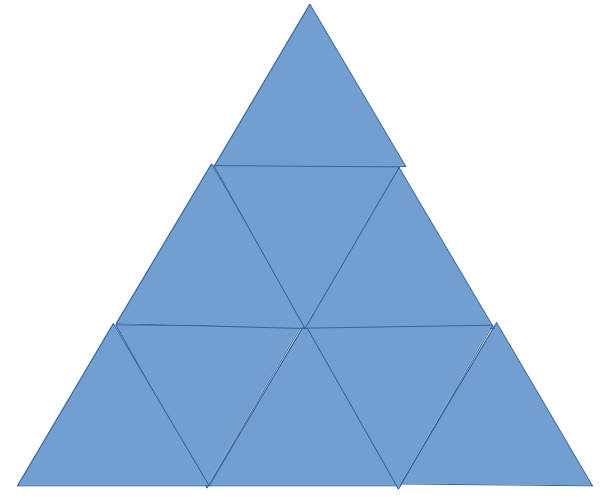
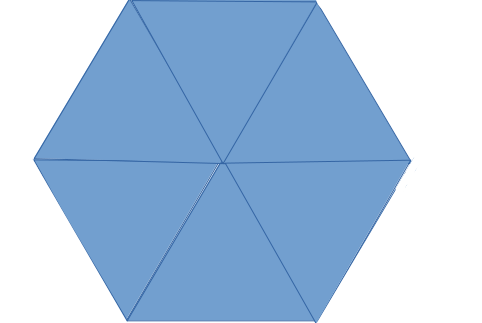
条件を満たさない例



入力
$N$
出力
ans
山本君の作ることのできる正多角形の面積の最大値を出力する。
出力の末尾には改行を入れること。
制約
- $1 \leq N \leq 10^{18}$
$N$は整数。
入出力例
例1
入力
1
出力
1
解説
正三角形1個で正三角形をつくることができる。(条件を満たす例の一番左のもの)
例2
入力
8
出力
6
解説
正三角形6個で正六角形を作ることができる。(条件を満たす例の一番右のもの)
例3
入力
999999999999999999
出力
999999998000000001