問題
二次元座標平面上に $4$ つの点 $a,b,c,d$ がある。
点 $a$ の座標は $(0,0)$ 、点 $b$ の座標は $(x_b,0)$ 、点 $c$ の座標は $(x_c,y_c)$ 、点 $d$ の座標は $(x_d,-y_d)$ である。
この $4$ 点を結ぶ四角形の面積を求めよ。なお、四角形の面積は整数となることが保障される。
入力
入力は以下の形式で標準入力から与えられる。$x_b$ $x_c$ $y_c$ $x_d$ $y_d$
出力
四角形の面積を整数で出力せよ。
出力の末尾には改行を入れること。
制約
- $2 \leq x_b \leq 100$
- $1 \leq x_c,x_d \lt x_b$
- $1 \leq y_c,y_d \leq 100$
- 入力は全て整数である。
- 四角形の面積が整数とならないような入力は与えられない。
入出力例
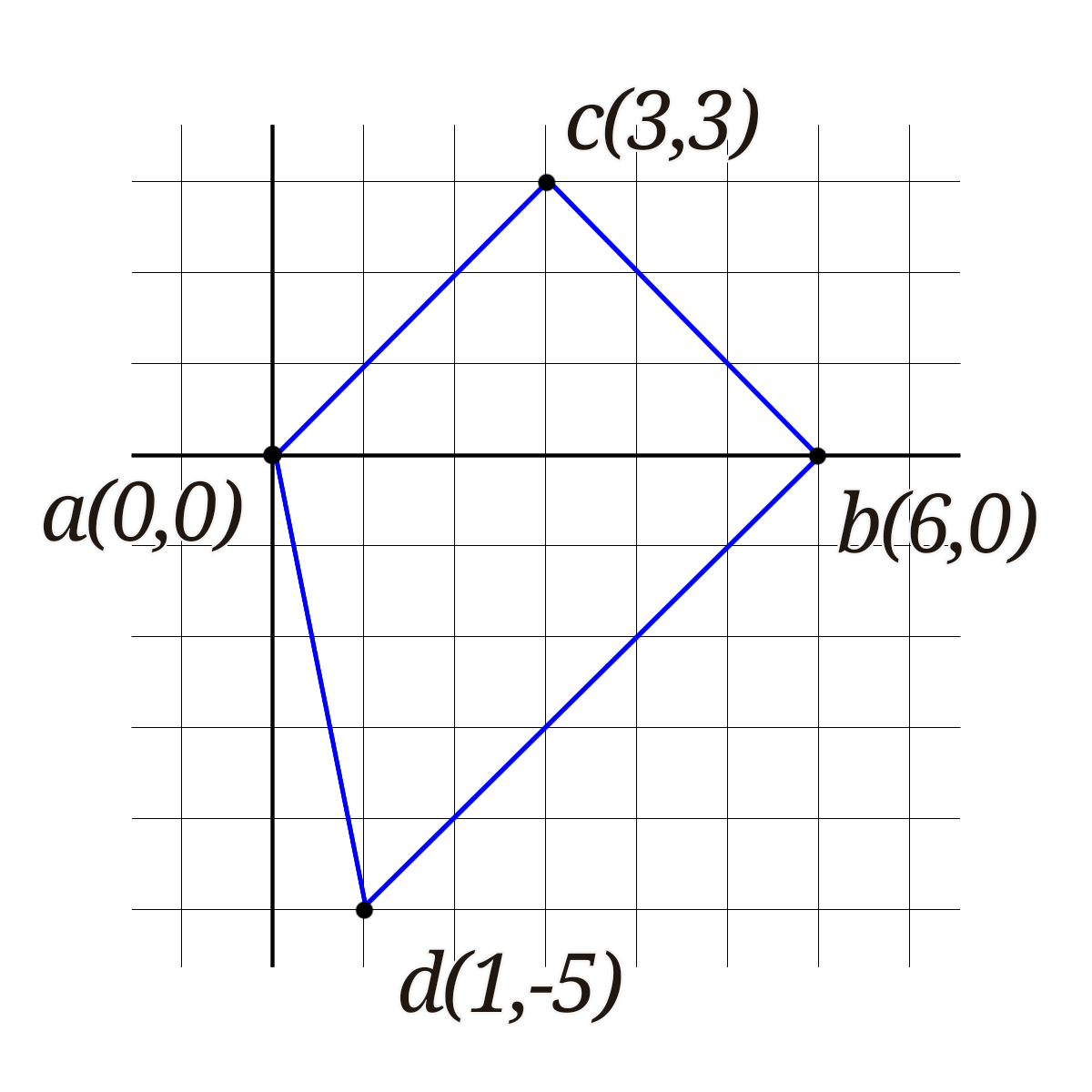
入力例1
6 3 3 1 5
出力例1
24
下図のような四角形となる。
入力例2
2 1 100 1 100
出力例2
200