問題
$V_1$ 頂点 $E_1$ 辺のグラフ $G_1$ と $V_2$ 頂点 $E_2$ 辺のグラフ $G_2$ があり、それぞれの頂点には $1,2,\ldots,V_1 \ , \ 1,2,\ldots,V_2$ の番号がつけられています。また、$i$ 番目の辺は $G_1$ の頂点 $u_{1_i}$ と $v_{1_i}$ を双方向に結び、$G_2$ の頂点 $u_{2_i}$ と $v_{2_i}$ を双方向に結んでいます。
$G_1$ の頂点 $X$ と、$G_2$ の頂点 $Y$ をそれぞれ $1$ つずつ選ぶとき、以下のような条件を満たす $X,Y$ の組はいくつあるでしょうか?
- 頂点 $X$ と頂点 $Y$ を双方向に結ぶ辺をひとつ追加したとき、$G_1$ の頂点 $s$ から $G_2$ の頂点 $g$ への距離は $L$ である。
なお、この問題での頂点 $s$ から頂点 $g$ への距離とは、頂点 $s$ から頂点 $g$ へ辿り着くために通る必要のある最小の辺の個数である。
入力
入力は以下の形式で標準入力から与えられる。
$V_1 \ E_1 \ V_2 \ E_2$
$s \ g \ L$
$u_{1_1} \ v_{1_1}$
$u_{1_2} \ v_{1_2}$
$\vdots$
$u_{1_{E_1}} \ v_{1_{E_1}}$
$u_{2_1} \ v_{2_1}$
$u_{2_2} \ v_{2_2}$
$\vdots$
$u_{2_{E_2}} \ v_{2_{E_2}}$
出力
条件を満たす $X,Y$ の組の個数を出力せよ。
出力の末尾には改行を入れること。
制約
- $1 \leq V_1,V_2 \leq 10^5$
- $V_1 - 1 \leq E_1 \leq \min(10^5, \frac{V_1(V_1 - 1)}{2})$
- $V_2 - 1 \leq E_2 \leq \min(10^5, \frac{V_2(V_2 - 1)}{2})$
- $1 \leq s \leq V_1$
- $1 \leq g \leq V_2$
- $1 \leq L \leq 2 \times 10^5$
- $1 \leq u_{1_i},v_{1_i} \leq V_1$
- $1 \leq u_{2_i},v_{2_i} \leq V_2$
- $G_1,G_2$ はそれぞれ連結なグラフであり、自己辺や多重辺を含まない。
- 入力は全て整数である。
入出力例
入力例1
4 4 5 4 1 5 4 1 2 1 3 2 3 3 4 1 2 2 4 3 4 4 5
出力例1
6
$G_1$ と $G_2$ は下図のようなグラフになります。
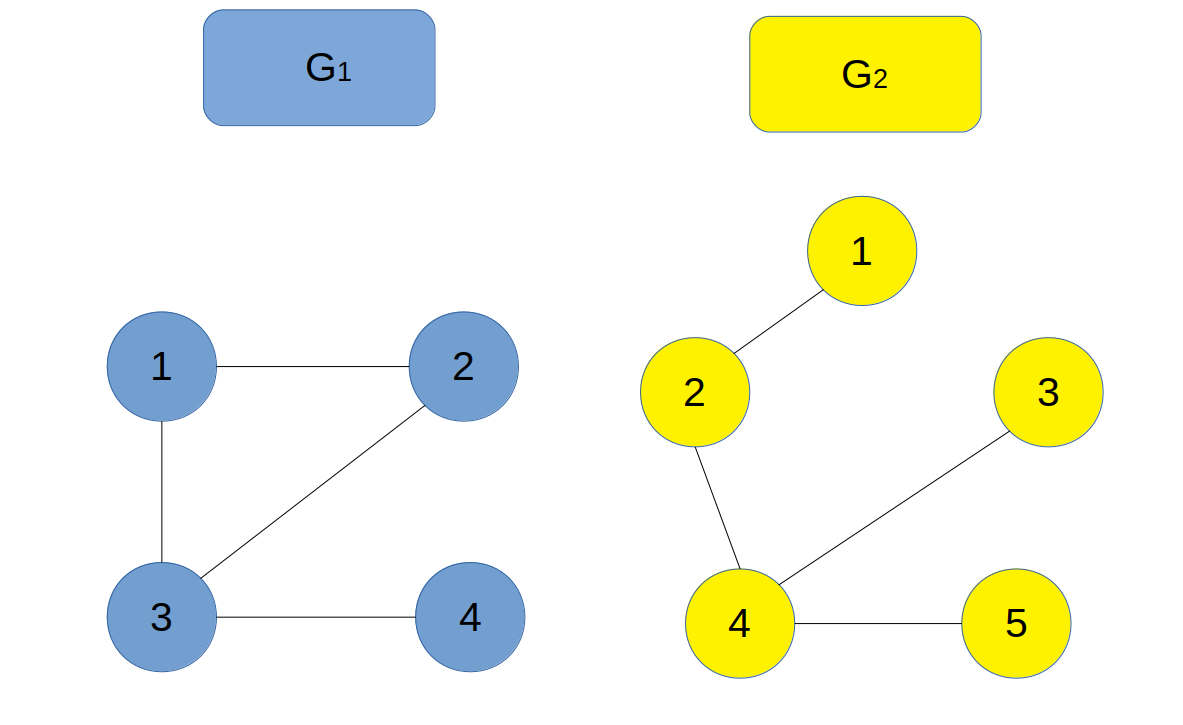
このとき、条件を満たす $X,Y$ の組は $(1,1),(2,2),(2,3),(3,2),(3,3),(4,4)$ の $6$ つです。
例として、 $(X,Y) = (4,4)$ のとき、下図のようになります。
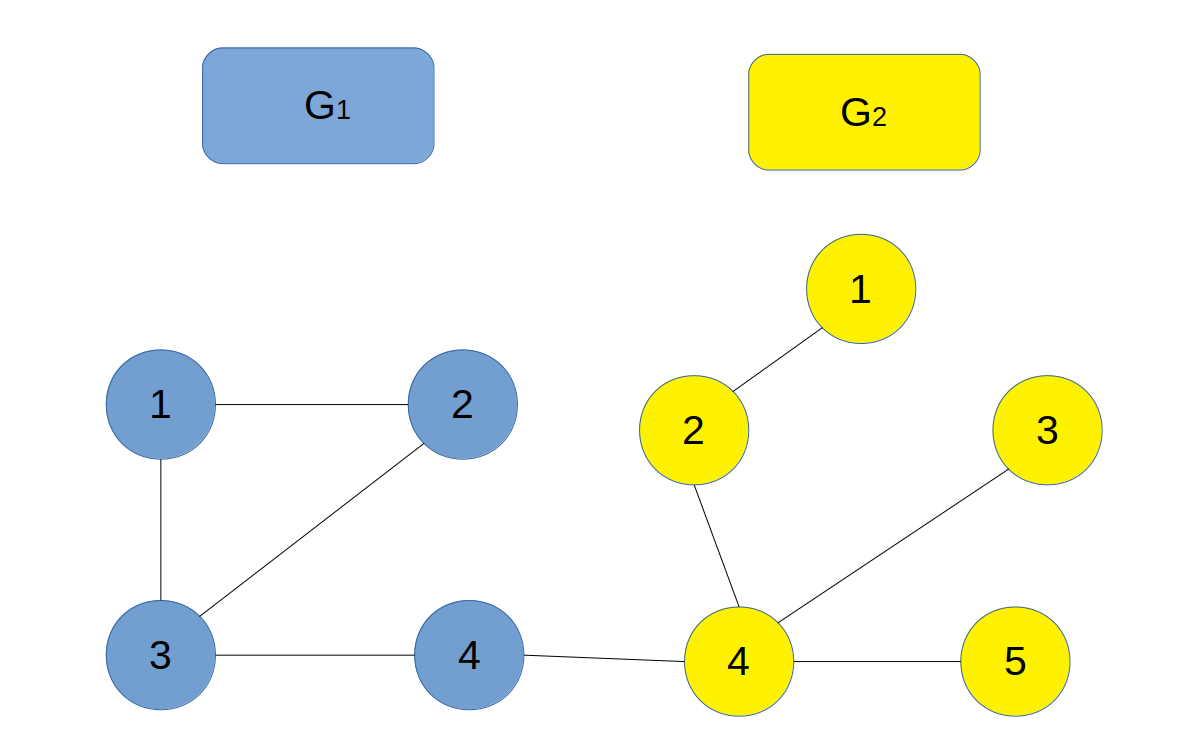
このとき、$G_1$ の頂点 $1$ から $G_2$ の頂点 $5$ への距離は $4$ となるため条件を満たします。
入力例2
3 2 1 0 2 1 100 3 1 2 1
出力例2
0
条件を満たす $X,Y$ の組は存在しないため、$0$ を出力します。
出力例3
8 14 6 5 8 5 5 6 2 2 3 5 6 1 8 5 3 8 5 1 4 2 8 7 2 6 1 2 4 3 1 2 1 7 4 5 2 1 2 5 3 1 6 6 4
出力例3
8