問題
山田之国には東西方向にまっすぐに伸びる$ \ H \ $本の道路と、南北方向にまっすぐに伸びる$ \ W \ $本の道路があります。
北から$ \ Y \ (1 \leq Y \leq H) \ $番目、西から$ \ X \ (1 \leq X \leq W) \ $番目の道路との交差点を$ \ (Y, X) \ $と表します。
山本君は交差点$ \ (1,1) \ $の近くに住んでおり、交差点$ \ (H,W) \ $の近くの「山田うどん」という店へと向かいたいです。
山本君は道路上を移動することができますが、東または南に向かって移動することしかできません。
また、道路を通過するためには事前に通行料を払っておかねばならず、一度払えば何度でも通ることができます。このとき、交差点を通過するだけであれば通行料を払う必要はありません。
北から$ \ Y \ $番目の道路の通行料は$ \ C_Y \ $であり、西から$ \ X \ $番目の道路の通行料は$ \ C_{H+X} \ $です。
山本君が交差点$ \ (1,1) \ $から交差点$ \ (H,W) \ $へ辿り着くために支払わなければならない通行料の最小値を求めてください。
入力
入力は以下の形式で標準入力から与えられる。
$H \ W$
$C_1$
$C_2$
$\vdots$
$C_H$
$C_{H+1}$
$\vdots$
$C_{H+W}$
出力
支払わなければならない通行料の最小値を出力せよ。出力の末尾には改行を入れること。
制約
- $1 \leq H,W \leq 5 \times 10^3$
- $1 \leq C_i \leq 10^9 \ (1 \leq i \leq H + W)$
- 入力はすべて整数。
入出力例
入力例1
3 3 20 60 30 90 20 70
出力例1
70
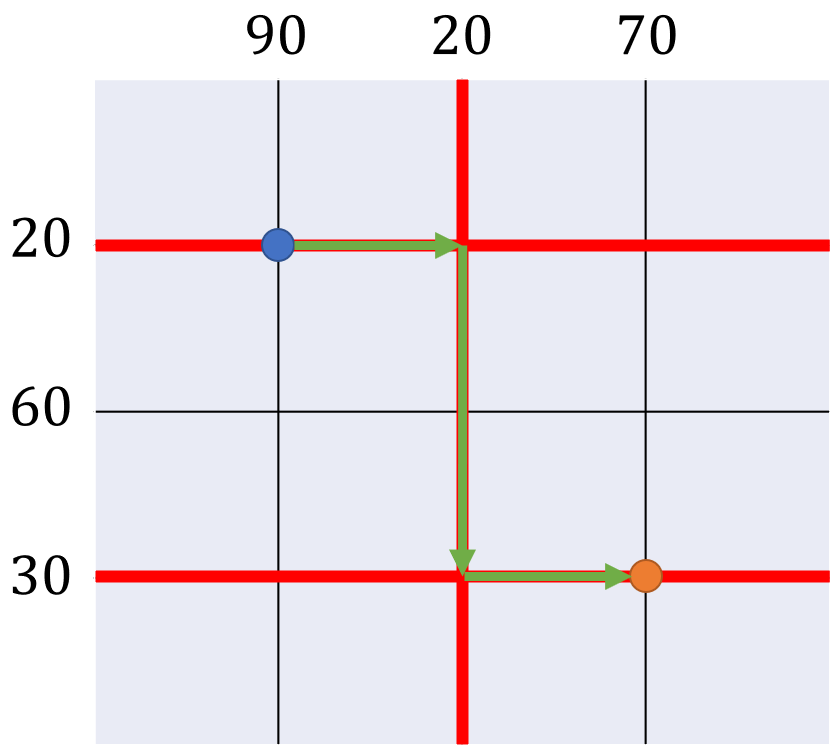
例として、以下のように赤色の道路の通行料を支払い、緑色の矢印のように進むことで支払う通行料は$ \ 20 + 20 + 30 = 70 \ $となりこれが最小です。
このとき、北から$ \ 2 \ $本目の道路は交差点を通過しているだけなので通行料を支払う必要はありません。西から$ \ 1,3 \ $番目の道路も同様です。