注意
この問題は実行時間が厳しめに設定されています。高速な言語でチャレンジしてみてください。
問題
$H \ $行$ \ W \ $列のグリッドがあり、上から$ \ y \ $番目、左から$ \ x \ $番目のマスをマス$ \ (y,x) \ $と表します。$ \ S_{i,j} \ $が.であるときマス$ \ (i,j) \ $は白色で塗られており#であるとき黒色で塗られています。
マス$ \ (s_y,s_x) \ $に駒「竜王」が置かれており、この駒は$ \ 1 \ $手で次のような$ \ 2 \ $種類の動きができます。
(〇のついたマスへ移動できます)
| 移動1 | 移動2 |
|---|---|
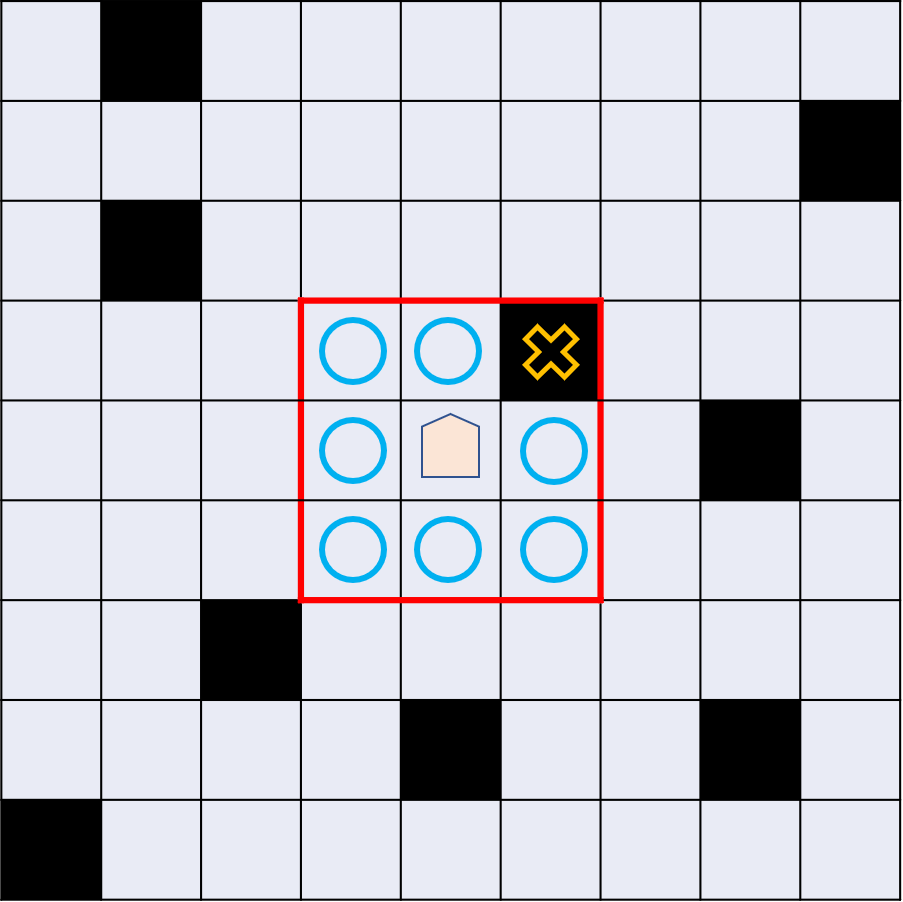 |
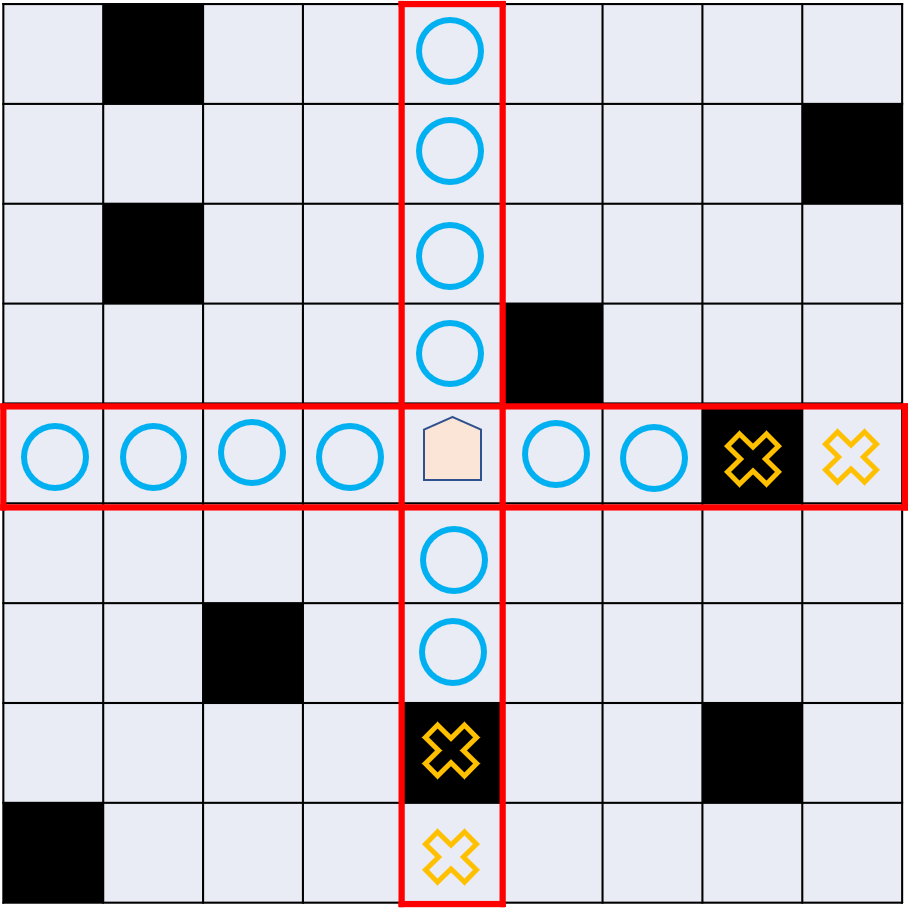 |
より正確には、竜王がマス$ \ (a,b) \ $にあるとき、次の$ \ 2 \ $種類の移動が可能です。
- 移動1: $|a - c| + |b - d| \leq 1 \ $を満たすマス$ \ (c,d) \ $へ移動する
- 移動2: $a = c \ $又は$ \ b = d \ $を満たすマス$ \ (c,d) \ $へ移動する
ただし移動2を行う場合、移動元のマスと移動先のマスの間に黒いマスが存在するような移動はできません。また、移動1,2ともに黒いマスへ移動させることはできず、グリッドの外に移動させることもできません。
竜王をマス$ \ (s_y,s_x) \ $からマス$ \ (g_y,g_x) \ $に動かすのに必要な最小手数を求めてください。
入力
入力は以下の形式で標準入力から与えられる。
$H \ W$
$s_y \ s_x \ g_y \ g_x$
$S_{1,1} S_{1,2} \ldots S_{1,W}$
$S_{2,1} S_{2,2} \ldots S_{2,W}$
$\vdots$
$S_{H,1} S_{H,2} \ldots S_{H,W}$
出力
動かすのに必要な最小手数を出力せよ。ただし、マス$ \ (g_y,g_x) \ $に動かすことが不可能である場合は$ \ -1 \ $を出力せよ。
出力の末尾には改行を入れること。
制約
全ての入出力ケースについて以下を満たす。
- $1 \leq H,W \leq 1500$
- $1 \leq s_y,g_y \leq H$
- $1 \leq s_x,g_x \leq W$
- $(s_y,s_x) \neq (g_y,g_x)$
- $S_{i,j} \ $は
.又は#のいずれかである - $S_{s_y,s_x} \neq $
# - $S_{g_y,g_x} \neq $
# - $H,W,s_y,s_x,g_y,g_x \ $は整数
入出力例
入力例1
4 5 1 1 4 4 ..... ##.## ##.## ###.#
出力例1
3
入力例2
3 3 1 2 3 3 ... .## ##.
出力例2
-1