問題
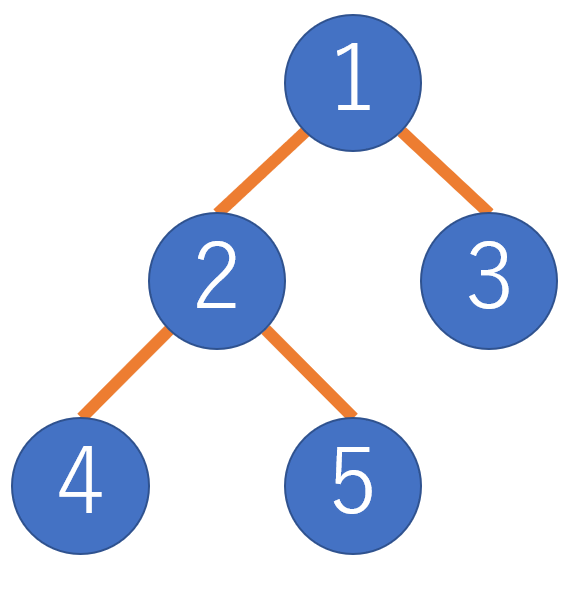
$N \ $個の頂点からなる根付き木があります。頂点$ \ 1 \ $が根であり、頂点$ \ i \ (2 \leq i \leq N) \ $の親は頂点$ \ \left \lbrack \frac{i}{2} \right \rbrack \ $です。
頂点$ \ i \ $とその頂点の親を結ぶ辺を辺$ \ i \ $としたとき、辺$ \ i \ $を通るには次の条件を満している必要があります。
- $p_i = 0 \ $のとき、辺$ \ e_i \ $を偶数回通っている
- $p_i = 1 \ $のとき、辺$ \ e_i \ $を奇数回通っている
次のような質問が$ \ Q \ $回にわたって与えられます。順に答えてください。
- 頂点$ \ s_j \ (1 \leq j \leq Q) \ $から頂点$ \ t_j \ $に辿り着くことはできますか?
入力
入力は以下の形式で標準入力から与えられる。
$N$ $p_2 \ e_2$ $p_3 \ e_3$ $\vdots$ $p_N \ e_N$ $Q$ $s_1 \ t_1$ $s_2 \ t_2$ $\vdots$ $s_Q \ t_Q$
出力
各質問について、辿り着くことができるならばYes、できないならばNoを改行区切りで出力せよ。
制約
- $2 \leq N \leq 10^5$
- $1 \leq Q \leq 10^5$
- $p_i \in \{0,1\}$
- $2 \leq e_i \leq N$
- $1 \leq s_j,t_j \leq N$
- $s_j \neq t_j$
- 入力は全て整数
入出力例
入力例1
5 1 3 0 2 1 2 1 5 3 3 4 4 5 4 3
出力例1
Yes No No
$1 \ $つ目の質問では、辺$ \ 3 \to \ $辺$ \ 2 \to \ $辺$ \ 4 \ $の順番に通れば頂点$ \ 4 \ $に辿り着くことができます。
$2,3 \ $つ目の質問では、どのように移動しても目的の頂点に辿り着くことはできません。
入力例2
10 1 4 1 2 0 4 0 3 1 10 1 9 0 7 0 4 0 7 5 3 10 9 7 7 8 10 8 9 3
出力例2
No Yes No Yes Yes