問題
$N \ $頂点$ \ M \ $辺のグラフがあります。各頂点には色が塗られており、頂点$ \ i \ (1 \leq i \leq N) \ $は色$ \ C_i \ $で塗られています。
$j \ (1 \leq j \leq M) \ $番目の辺は頂点$ \ u_j \ $と頂点$ \ v_j \ $を結ぶ長さ$ \ l_j \ $の無向辺です。
山本君はこのグラフの頂点の色を$ \ Q \ $回にわたって塗り替えます。
$k \ (1 \leq k \leq Q) \ $回目の操作では、頂点$ \ x_k \ $を色$ \ c_k \ $に塗り替えます。
各操作直後のグラフについて以下の値を求めてください。
- 頂点$ \ 1 \ $からの最短経路長が$ \ L \ $以下である頂点に塗られている色の種類数が$ \ K \ $以上となるような最小の非負整数$ \ L $。
入力
入力は以下の形式で標準入力から与えられる
$N \ M \ Q \ K$ $C_1 \ C_2 \ldots C_N$ $u_1 \ v_1 \ l_1$ $u_2 \ v_2 \ l_2$ $\vdots$ $u_M \ v_M \ l_M$ $x_1 \ c_1$ $x_2 \ c_2$ $\vdots$ $x_Q \ c_Q$
出力
出力は$ \ Q \ $行からなる。
$k \ $行目には$ \ k \ $回目の操作が終了した直後のグラフについて条件を満たす最小の非負整数$ \ L \ $を出力せよ。
ただし、条件を満たす$ \ L \ $が存在しない場合は$ \ -1 \ $を出力せよ。
制約
- $1 \leq N \leq 10^5$
- $0 \leq M \leq \min(\frac{N(N-1)}{2},10^5)$
- $1 \leq Q \leq 10^5$
- $1 \leq K \leq N$
- $1 \leq C_i \leq 10^5$
- $1 \leq u_j,v_j \leq N$
- $1 \leq l_j \leq 10^9$
- $1 \leq x_k \leq N$
- $1 \leq c_k \leq 10^5$
- 与えられるグラフは連結かつ単純である
- 入力は全て整数
入出力例
入力例1
5 5 2 3 1 2 2 4 5 1 2 2 1 3 1 2 3 1 3 4 2 4 5 1 3 3 1 2
出力例1
2 3
$1 \ $回目の操作直後のグラフは次のようになります。$L = 2 \ $とすると、最短経路長が$ \ 2 \ $以下の頂点(赤線で囲った頂点)に塗られている色の種類数が$ \ 3 \ $となるため$ \ L = 2 \ $は条件を満たします。また、$L \ $を$ \ 2 \ $未満にすることはできないので$ \ 2 \ $が答えとなります。
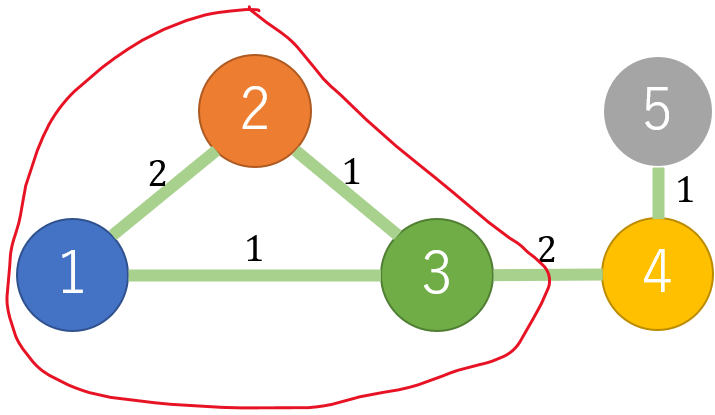
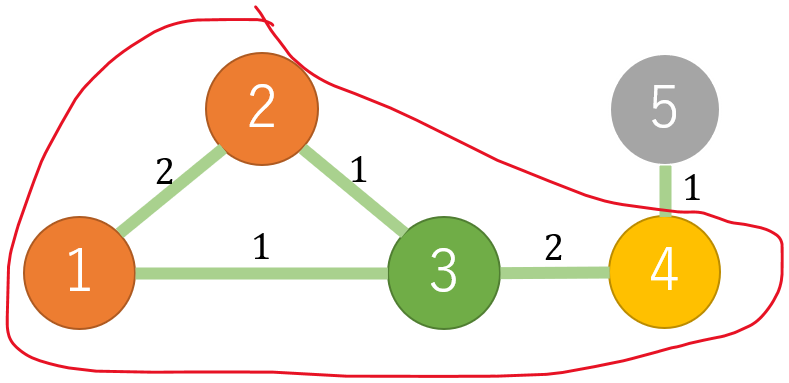
また、$2 \ $回目の操作直後のグラフは次のようになります。
入力例2
10 12 5 7 11 10 11 1 5 1 7 2 2 6 3 2 27 6 2 71 4 8 40 10 2 74 9 4 71 4 3 43 10 7 75 7 9 98 1 6 13 6 4 1 9 8 83 3 5 41 8 8 3 8 10 1 1 5 5 3
出力例2
158 158 183 -1 183