問題
二次元座標平面上に$ \ N \ $個の点があります。$i \ (1 \leq i \leq N) \ $番目の点の座標は$ \ (x_i,y_i) \ $です。
次の条件を満たす整数$ \ i,j \ $の組の個数を求めてください。
- $1 \leq i \lt j \leq N$
- 四角形$ \ (x_i,y_i),(x_i,y_j),(x_j,y_j),(x_j,y_i) \ $は正方形である。
入力
入力は以下の形式で標準入力から与えられる。
$N$ $x_1 \ y_1$ $x_2 \ y_2$ $\vdots$ $x_N \ y_N$
出力
条件を満たす整数$ \ i,j \ $の組の個数を出力せよ。出力の末尾には改行を入れること。
制約
全ての入出力ケースについて以下を満たす。
- $2 \leq N \leq 3 \times 10^5$
- $-10^9 \leq x_i,y_i \leq 10^9$
- $(x_i,y_i) \neq (x_j,y_j) \ (i \neq j)$
- 入力は全て整数
入出力例
入力例
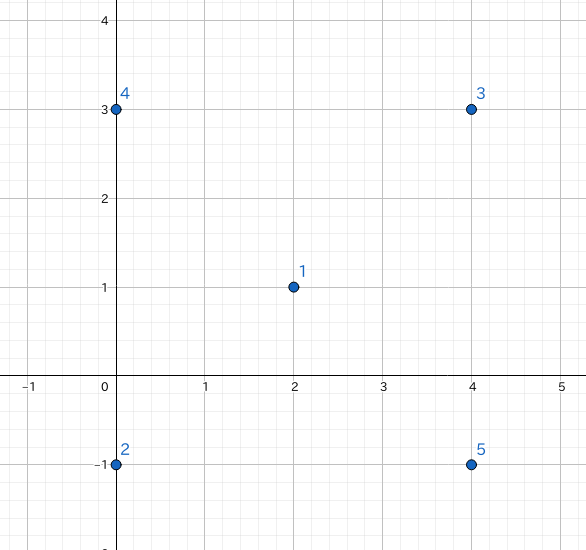
5 2 1 0 -1 4 3 0 3 4 -1
出力例
6
条件を満たす$ \ i,j \ $の組は$ \ (1, 2),(1,3),(1,4),(1,5),(2,3),(4,5) \ $の$ \ 6 \ $組です。