問題
福岡博士は面白いパネルを発明した. パネルの形は1単位の大きさの正方形で,その表面は黄・桃・赤・紫・緑・青のどれか一色である. そのパネルには次のような注目すべき二つの性質がある. 一つ目は,同じ色のパネルが隣接して配置されると, それらの縁がすこし融けてくっつく性質である. くっついたパネルは,1枚の多角形のパネルになる. 二つ目は パネルに電気ショックを与えるとパネルの色を 6色のうちの任意の1色に変更できる性質である. 色を指定するには電気ショックのパルスの波形を調節すればよい. 既に結合したパネルは電気ショックによりその全体の色が指定された一つの色 に変化する.
彼は,指定した色でパネルを多角形に結合させ, その結合後のパネルの大きさや色の違いによる強度の違いを, 単体のパネルの性質と比較して調べることにした.

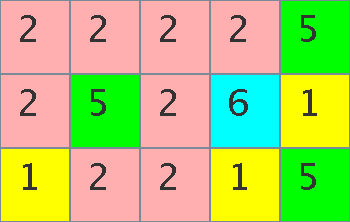
多くのパネルを基板の上で複雑な化学プロセスを経て同時に合成し生成するため, 製造したパネルはランダムに着色され, 基板上に長方形の形に並べられている (図C-1). なお,図C-1中の2個の紫(色4)のパネルは隣接しているので初期状態で既に 一つのパネルに結合されていることに注意されたい.
ある1枚のパネルに電極を装着して,そのパネルの色を最終的な色に 応じて順次変更することにより, 隣接するパネルを段々に合体させて, 指定した色のより大きな結合パネルを得ることができる. 残念ながらパネルに電気ショックを6回与えるとパネルは壊れてしまう. すなわち,色を変えることができる回数は5回である.
図C-1の左上角のパネルに電極を取りつけた場合を考える. 最初にパネルの色を黄色から青色に変えると,右隣のパネルと結合する (図C-2).

次に,左上の結合パネルを青色から赤色に変えると赤色の3単位の結合パネルになる (図C-3). さらに,同パネルを赤色から紫色に変えると,紫色の5単位の結合パネルに なる(図C-4).


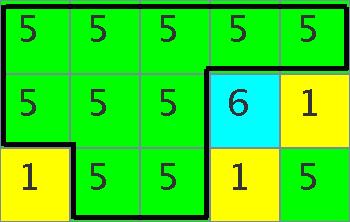
さらに続けて,紫色を桃色に変更して図C-5の桃色の結合パネルを経て, 桃色を緑色にすると図C-6の緑色の結合パネルが得られる. 緑色の結合パネルは10単位の正方形パネルからなる.
色々な大きさのパネルの強度を調べるために,指定した色でなるべく大きなパネルを結合したい. あなたの仕事は,指定された色の一番大きな結合パネルを得るための,5回の色の変更方法を見出すプログラムを書くことである.ただし,電極は左上角のパネルに固定されていることとする.
Input
入力は複数のデータセットからなり,それぞれが以下の形式である.
h w c
p1,1 p1,2 ... p1,w
p2,1 p2,2 ... p2,w
...
ph,1 ph,2 ... ph,w
h, wは8以下の正の整数であり,長方形の高さと幅を表す. cは6以下の正の整数であり,最終的に結合されるパネルの目標となる色を表す.pi,jは6以下の正の整数であり, (i, j)の場所の単位パネルの初期状態の色を表す.入力の終わりは,空白文字1個で区切られた3個のゼロのみからなる行で表される.
Output
各データセットについて,左上角のパネルの5回の色変更により,目標色となる左上角のパネルの最大の大きさが何単位にあたるかを1行に出力せよ.それ以外の余計な文字を含んではいけない.
Sample Input/Output
Sample Input
3 5 5 1 6 3 2 5 2 5 4 6 1 1 2 4 1 5 4 5 6 1 5 6 1 2 1 4 6 3 2 1 5 2 3 2 1 1 2 3 2 1 1 5 1 1 8 6 1 2 3 4 5 1 2 3 8 1 1 1 2 3 4 5 1 2 3 8 8 6 5 2 5 2 6 5 4 2 4 2 2 2 5 2 2 2 4 4 4 2 5 2 2 2 6 4 5 2 2 2 6 6 6 6 5 5 2 2 6 6 6 2 5 4 2 2 6 6 2 4 4 4 6 2 2 6 2 2 2 5 5 2 2 2 8 8 2 3 3 5 4 1 6 2 3 2 3 6 4 3 6 2 2 4 1 6 6 6 4 4 4 2 5 3 6 3 6 3 5 3 1 3 4 1 5 6 3 1 6 6 3 5 1 5 3 2 4 2 2 2 6 5 3 4 1 3 6 1 5 5 4 0 0 0
Output for the Sample Input
10 18 1 5 6 64 33