1650 - Delivery

問題

山田くんは荷物配達の仕事をしている。
今日は「メゾンヤマモト」というマンションに住む $N$ 人の山本くん（$N$ 個の部屋）に荷物を届けなければならない。
メゾンヤマモトとそれぞれの配達先については以下の情報がわかっている。

• メゾンヤマモトは $M$ 階建てである
• $i(1 \leq i \leq M)$ 階には配達先が $D_i$ 個あり、$R_{i, 1}, \cdots, R_{i, j}, \cdots, R_{i, D_i} (1 \leq j \leq D_i)$ の順で一直線に並んでいる
• 荷物を載せたトラックはメゾンヤマモトの入口（一般化のため部屋 $0$ と呼ぶことにする）に停まっている
• 部屋 $0$ は各階の先頭の部屋 $R_{i, 1}$ と隣接している
• 隣り合っている二つの部屋（部屋 $x, y$）間の移動には時間 $T_{x, y}$ がかかる $(1 \leq x, y \leq N)$
• 各階には部屋 $0$ からしか行けない

世の中にはバケモノじみた山田くんが存在するが、この山田くんは普通の人間であるため、一度の配達では $K$ 個の荷物までしか持つことができない。
このとき、全ての荷物を配達してトラックに戻るまでには、最低でもどれだけの時間が必要であるか。

入力

入力は以下の形式で標準入力から与えられる。

$N$ $M$ $K$
$D_1$
$R_{1, 1} \cdots R_{1, D_1}$
$T_{0, R_{1, 1}} \cdots T_{R_{1, D_1 - 1}, R_{1, D_1}}$
$\vdots$
$D_i$
$R_{i, 1} \cdots R_{i, D_i}$
$T_{0, R_{i, 1}} \cdots T_{R_{i, D_i - 1}, R_{i, D_i}}$
$\vdots$
$D_M$
$R_{M, 1} \cdots R_{M, D_M}$
$T_{0, R_{M, 1}} \cdots T_{R_{M, D_M - 1}, R_{M, D_M}}$

出力

全ての荷物を配達してトラックに戻るまでに必要な時間を出力せよ。出力の最後に改行を入れること。

制約

全ての入出力ケースについて以下を満たす。

• $5 \leq N \leq 10^5$
• $1 \leq M, K, R_{i, j} \leq N$
• $1 \leq D_i$
• $\sum_{1}^{M} D_i = N$
• $R_{i1, j1} \neq R_{i2, j2}(i1 \neq i2$ または $j1 \neq j2)$
• $1 \leq T_{x, y} \leq 10^5$

入出力例

入力例1

5 2 2
2
4 1
3 1
3
2 3 5
5 2 3

出力例1

38

与えられた情報を図で表すと以下のようになる。

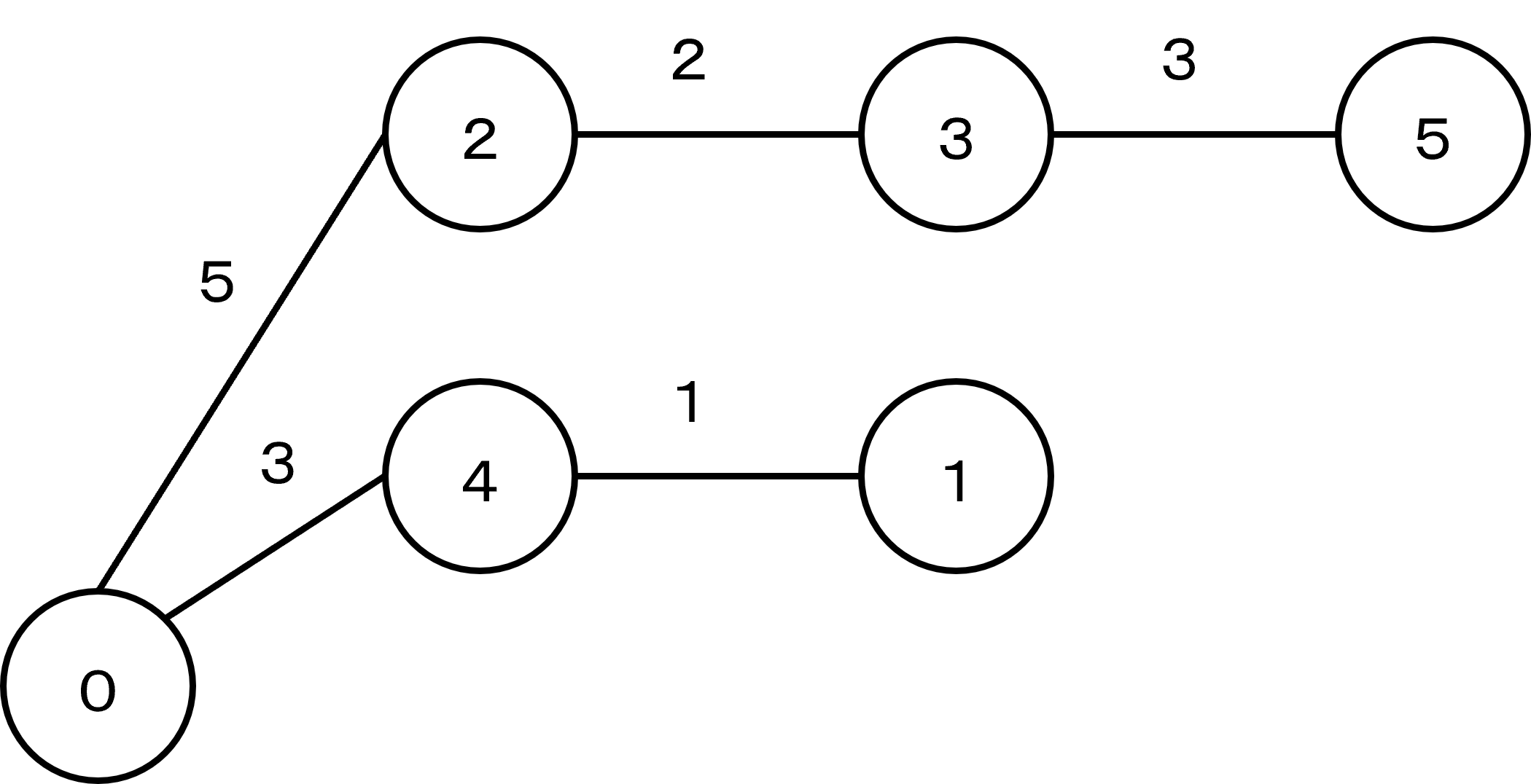
山田くんは一度に $2$ 個まで荷物を運べるため、「部屋 $1, 4$ に荷物を運ぶ」、「部屋 $3, 5$ に荷物を運ぶ」、「部屋 $2$ に荷物を運ぶ」の工程で全ての山本くんに荷物を届けることができる。
$T_{x, y}$ は片道の時間であり、最終的にかかる時間は往復の時間であることに注意すること。

---

入力例2

10 1 1
10
8 1 4 10 9 3 7 2 5 6
1 1 1 1 1 1 1 1 1 1

出力例2

110

部屋が全て１列に並んでいる場合も存在する。

---

入力例3

10 3 5
5
1 2 3 4 5
3 7 1 10 2
3
6 7 8
2 3 3
2
9 10
8 1

出力例3

80