問題
長さ$N$の配列$A_1 ...A_n$が与えられる。
この配列に対する$Q$個のクエリに答えてください。
クエリ
整数$P$が与えられる。 $B_i =A_i×(P-i+1)とするときの、B_1+...+B_Pの値を出力せよ。(1\leq P \leq N)$入力
入力は以下の形式で標準入力から与えられる。
$N$ $Q$ $A_1 ... A_N$
1行目に整数$N,Q$が与えられる。 2行目に整数列$A_1 ... A_n$が空白区切りで与えられる。
クエリの与えられ方は以下のとおりである。
$P$
1行に整数$P$が与えられる。
出力
出力の最後に改行を入れること。
制約
全ての入出力ケースについて以下を満たす。
- $1 \leq N\leq 2×10^{5}$
- $1 \leq Q\leq 2×10^{5}$
- $1 \leq A_i\leq 2×10^{5} (1\leq i \leq N)$
- $1 \leq P \leq N$
入出力例
入力例1
4 4
1 2 3 4
1
2
3
4
出力例1
1
4
10
20
P=1では、1×1=1
P=2では、1×2+2×1=4
P=3では、1×3+2×2+3×1=10
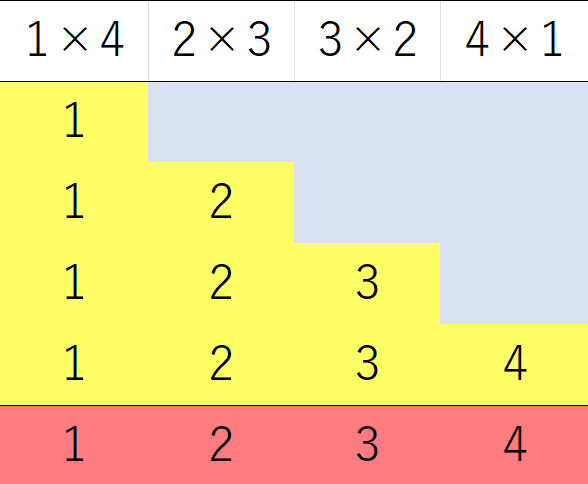
P=4では、1×4+2×3+3×2+4×1=20
が答えとなる。下図はP=4の場合を図示したものであり、黄色部分の総和が出力である。
入力例2
2 1
3000 3000
2
出力例2
9000