問題
HOJ国は$N$個の都市と、都市間をつなぐ$M$個の道路、$S$個の会社から成ります。
都市には、$1,2,...N$と番号が振られており、各都市には市民がちょうど$1$人います。
会社には、$1,2,...S$と番号が振られており、会社$i(1 \leq i \leq S)$は都市$A_i$にあり、給料は$B_i$です。
$i$個目の道路$(1 \leq i \leq M)$は、都市$U_i$と都市$V_i$をつないでおり、双方向に移動が出来ます。
都市$i$に住んでいる市民は、都市$i$と都市$A_j$がいくつかの道路を経由して行き来可能な時、会社$j$で働くことが出来ます。
この時、この市民の幸福度は、都市$i$から都市$A_j$へ行く時に通る道路の数の最小値を$dist(i,A_j)$として、
・$MAX(0,B_j - dist(i,A_j))$
になります。
各市民が働く会社を自由に1つ決めることが出来る時、HOJ国の市民の幸福度の総和の最大値を求めてください。
入力
入力は以下の形式で標準入力から与えられる。
$N$ $M$ $S$ $A_1$ $B_1$ $A_2$ $B_2$ ... $A_S$ $B_S$ $U_1$ $V_1$ $U_2$ $V_2$ ... $U_M$ $V_M$
1行目に整数$X$が与えられる。 2行目に整数$Y$が与えられる。
出力
出力の最後に改行を入れること。
制約
全ての入出力ケースについて以下を満たす。
- $1 \leq N,S \leq 2×10^5$
- $0 \leq M \leq 2×10^5$
- $1 \leq A_i \leq N (1 \leq i \leq N)$
- $1 \leq B_i \leq 10^9 (1 \leq i \leq N)$
- $1 \leq U_i,V_i \leq N (1 \leq i \leq N)$
- $ U_i≠V_i (1 \leq i \leq N)$
- 入力はすべて整数
入出力例
入力例1
5 4 2 1 2 5 3 1 2 2 3 3 4 4 5
出力例1
9
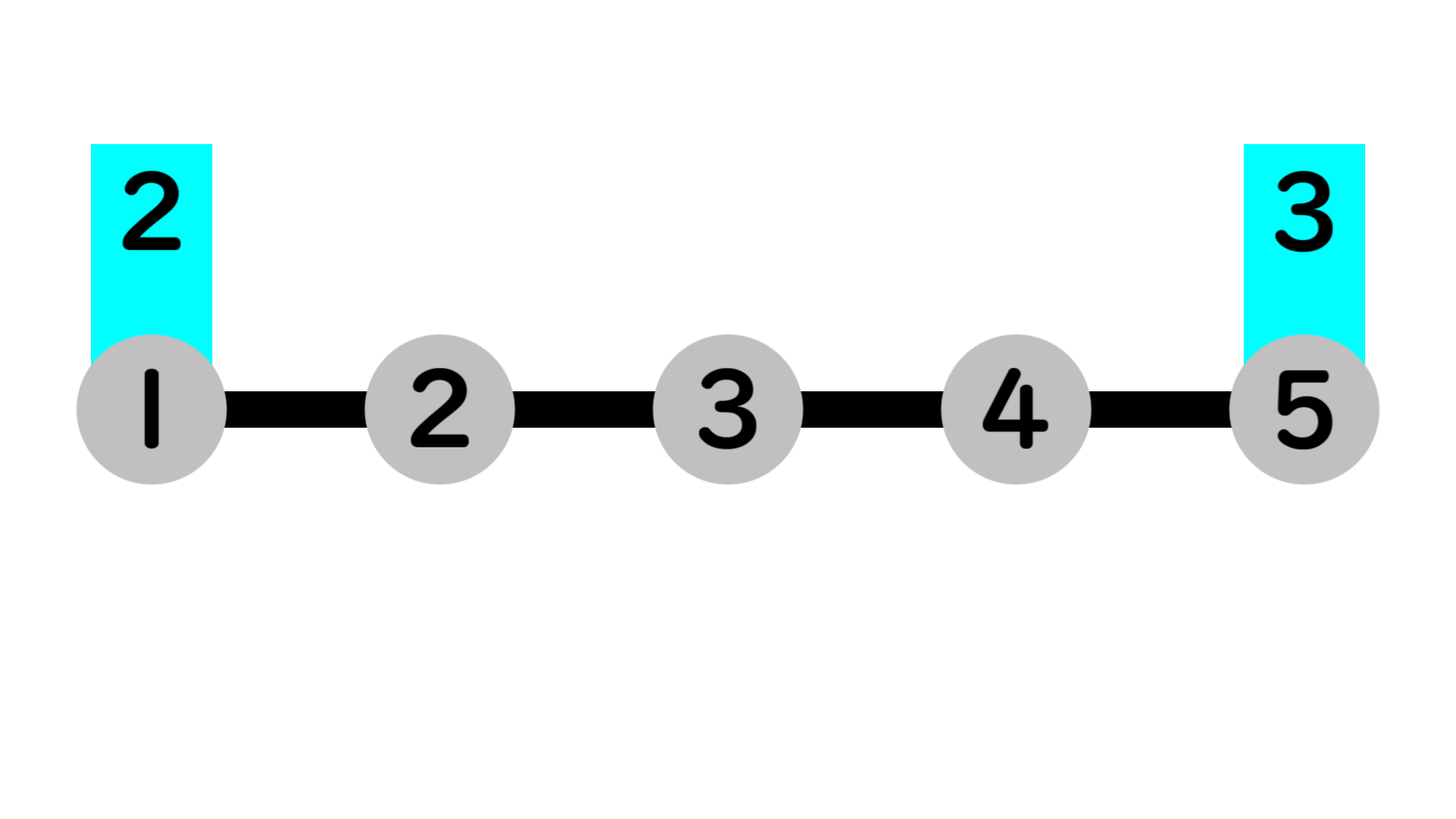
図は入力例1を簡易的に表したものです。
今回の場合、都市1,2の市民は会社1、都市3,4,5の市民は会社2で働くことで、各市民の幸福度は2,1,1,2,3となり、総和は9です。
総和を10以上にすることはできないので、9を出力してください。
入力例2
9 7 4 9 100 8 5 6 1 1 3 1 2 2 3 3 4 4 5 5 2 7 6 8 7
出力例2
119
任意の都市間を必ず移動できるとは限らないことに注意してください。答えがint型に収まるとは限りません。