前置き

夏祭りといえば...?

問題

ということで、パンケーキを五等分に切り分けることを考える。
パンケーキは円筒形のお菓子である。パンケーキには$N$箇所にのみ切れ込みが入っており、切れ込みのある位置でのみパンケーキを切ることが可能である。
切れ込みと切れ込みの間の部分に、時計回りに順に$1$から$N$の番号をふる。
ここで、$i$番目の「切れ込みと切れ込みの間の部分」の大きさは$A_i$である。

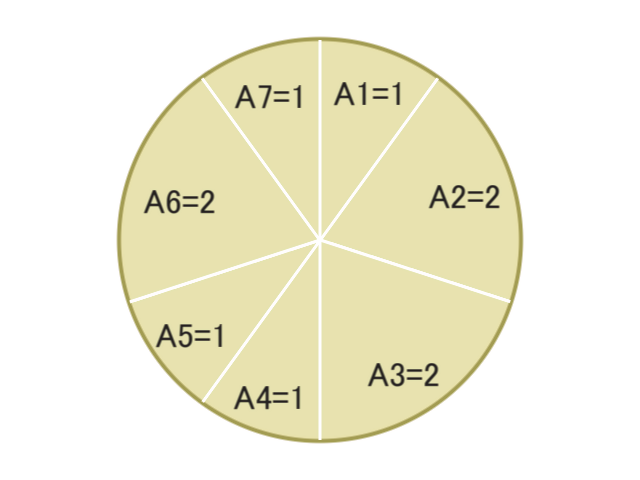
※上図はこの問題で考えられるパンケーキの一例(N=7)である。
このパンケーキの切れ込みから相異なる5箇所を選んでパンケーキを切ることで、大きさが等しい5つのパンケーキに分割することが出来るか判定してください。
$T$個のパンケーキがあるので、それぞれについて上記の問題を解いてください。

入力

入力は以下の形式で標準入力から与えられる。

$T$
$case_1$
$case_2$
...
$case_T$

1行目に整数$T$が与えられる。 2行目から$2×T$行にかけてパンケーキの情報が与えられる。

各ケースは以下の形式で標準入力から与えられる。

$N$
$A_1$ $A_2$ ... $A_N$

1行目に整数$N$が与えられる。 2行目に整数列$A$が与えられる。

例として、下の入力は問題文中の図のパンケーキを表す。

7
1 2 2 1 1 2 1

出力

パンケーキを五等分に出来るならYes、出来ないならNoを出力せよ。 出力の最後に改行を入れること。

制約

全ての入出力ケースについて以下を満たす。

• $1 \leq T \leq 5$
• $5 \leq N \leq 10^{5}$
• $1 \leq A_i \leq 10^{5}(1 \leq i \leq N)$

入出力例

入力例1

5
5
50 50 50 50 50
7
1 2 2 1 1 2 1
6
2 2 2 2 2 1
15
1 9 8 4 2 4 11 6 4 8 10 10 2 3 14
6
12 12 3 9 12 12

出力例1

Yes
Yes
No
No
Yes

2つ目のパンケーキについて、パンケーキは円筒形なので、{$A_7,A_1$},{$A_2$},{$A_3$},{$A_4,A_5$},{$A_6$}の5つに分割することができ、これは丁度五等分となっています。