問題
oさんは、ゲームで遊んでいる。このゲームは、お題となる効果音や動物の鳴き声をプレイヤーが声真似してマイクに録音し、
その声真似の精度をゲームのプログラムが測定し、点数が出るというものである。
このゲームで高得点を出したいoさんは得点の出方を調べた結果、以下のことが分かった。
お題となる音源を$M$,プレイヤーが録音した音源を$P$とする。
各音源を$N$個の均等な区間に分け、各区間の(平均の)音の高さを$M_i,P_i (1\leq i \leq N)$とする。
ここで、二次元平面上において、
点($0$,$0$) , ($1$,$M_1$) , ($2$,$M_2$) , ... , ($N$,$M_N$) , ($N+1$,$0$) , ($0$,$0$)をこの順に線分で結んで出来る領域を$S_M$,
点($0$,$0$) , ($1$,$P_1$) , ($2$,$P_2$) , ... , ($N$,$P_N$) , ($N+1$,$0$) , ($0$,$0$)をこの順に線分で結んで出来る領域を$S_P$,
としたとき、
$\displaystyle 得点 = max(100 - \frac{(\overline {S_M} \cap S_P) \cup (S_M \cap \overline {S_P})の面積}{S_Mの面積} \times 100 , 0)$
となる。
さて、お題となる音源$M$と、oさんがが録音した音源$P$の情報が与えられる。このときのoさんの声真似の点数を求めよ。
入力
入力は以下の形式で標準入力から与えられる。
$N$ $M_1$ $M_2$ ... $M_N$ $P_1$ $P_2$ ... $P_N$
1行目で分けられる区間の数$N$が与えられる。
2行目では、各区間におけるお題となる音源の音の高さ$M_i(1\leq i \leq N))$が与えられる。
3行目では、各区間におけるoさんが録音した音源の音の高さ$P_i(1\leq i \leq N))$が与えられる。
出力
oさんの声真似の点数を実数で求めよ。誤差は $ 10^{-4} $ まで許容される。出力の最後に改行を入れること。
制約
全ての入出力ケースについて以下を満たす。
- $ 1\leq N \leq 10^{5}$
- $ 1\leq M_i,P_i \leq 10^{9}$
- 入力される値は全て整数である。
- 任意の$ j (1\leq j \leq N-1)$について、$ M_j < P_j $ ならば $M_{j+1}\leq P_{j+1}$
- 任意の$ j (1\leq j \leq N-1)$について、$ P_j < M_j $ ならば $P_{j+1}\leq M_{j+1}$
入出力例
入力例1
4 1 1 1 1 1 2 2 1
出力例1
50.000000
出力例1の入力を図示すると、次のようになる。
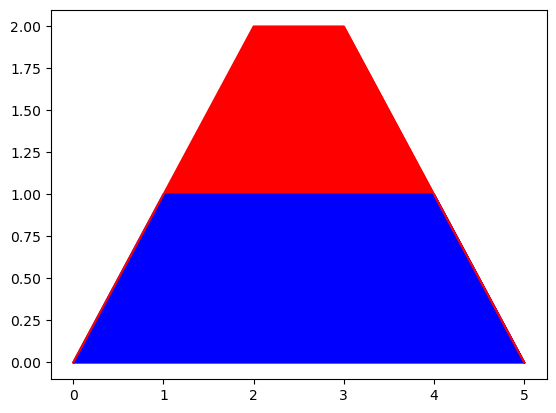
この図において、赤い部分が$(\overline {S_M} \cap S_P) \cup (S_M \cap \overline {S_P})$を、青い部分が$S_M$を表している。
入力例2
5 1 2 3 4 5 5 5 5 5 5
出力例2
33.333333
入力例3
5 5 5 5 5 5 5 5 5 5 5
出力例3
100.000000
でました!$100$点です!
入力例4
5 1 1 1 1 1 5 5 5 5 5
出力例4
0.000000
あれ?