2069 - Shoji Run

問題

障子がある。
格子が交差する点を頂点とし，頂点同士を繋ぐ部分を辺とする。
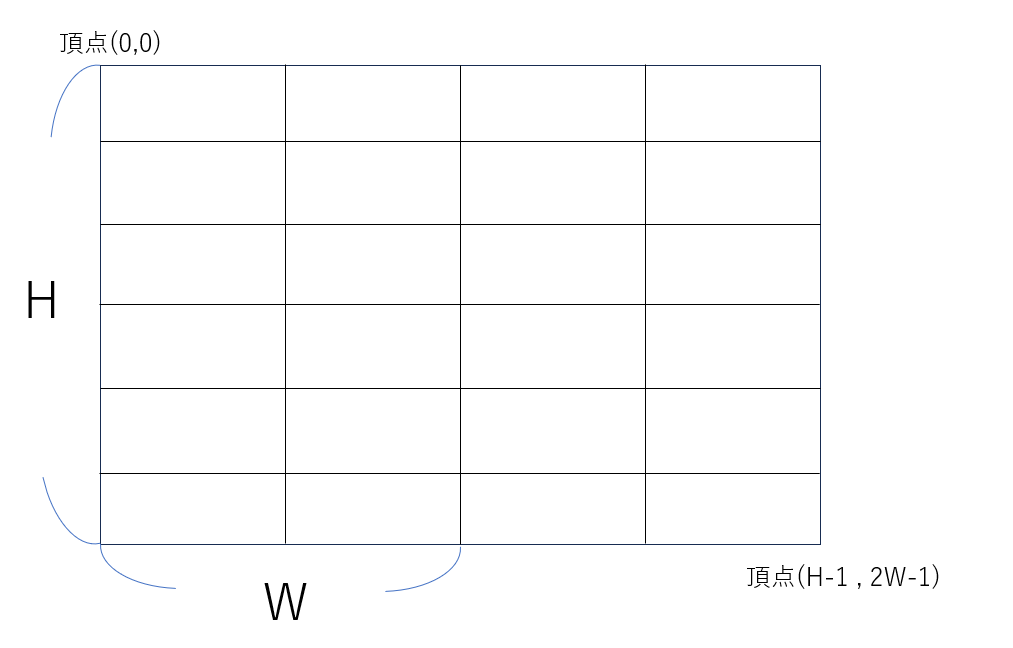
頂点の数が$H$×$W$の障子が2つあり，閉ざされている。
座標(0,0)から2枚の障子上の対角線まで移動したい。
各辺にはコストが定められていて，辺を移動するにはコストを支払わなければならない。
また，障子は1つ辺を通過するたびに開閉状態が変化する。
最小のコストで，座標(0,0)から対角線上の場所まで移動せよ。
厳密には，左右に2枚ある障子の内左側の障子の左上を頂点(0,0)とした時，辺を通過する度に障子が通行可能/不可能になるという条件の元で右側の障子の右下の頂点を頂点($H$,$2W$)とした時の頂点(0,0)から頂点($H-1$,$2W-1$)まで移動する時に合計で支払うコストの最低値を求めよ。

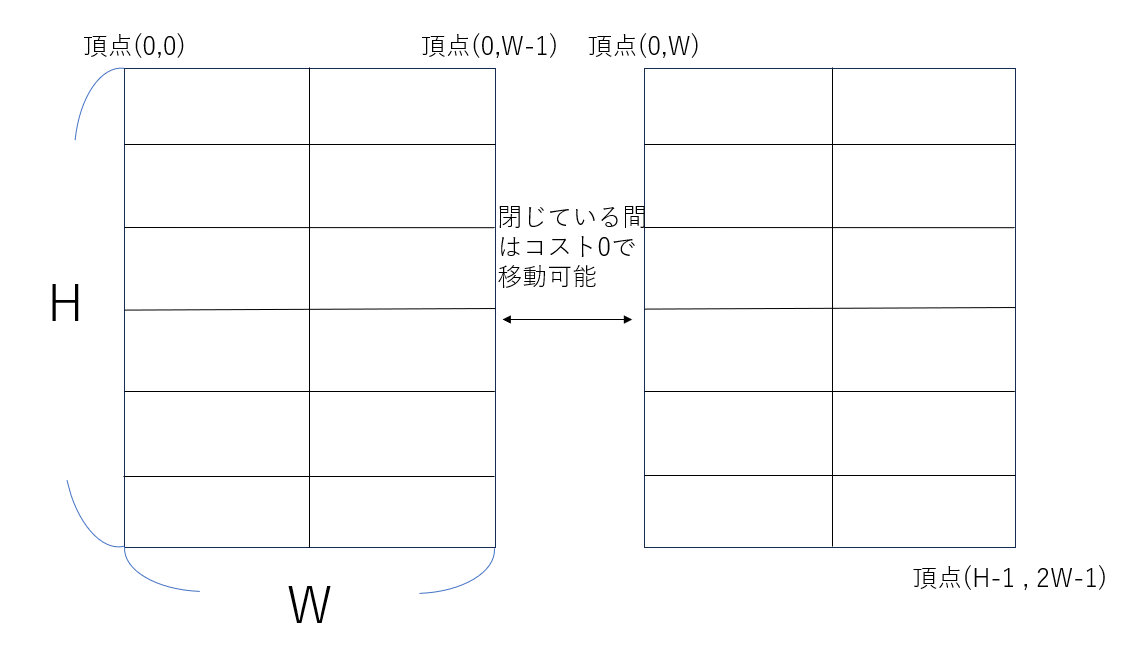
また最初に座標(0,0)に居る段階では障子は閉じていて，辺を移動するたびに開いている状態と入れ替わる。
閉じている状態では左右の障子間を行き来できるが，開いている状態では行き来できない。

閉じている状態

開いている状態

入力

入力は以下の形式で標準入力から与えられる。

$H$ $W$
$C_{0,0}, C_{0,1}, C_{0,2}, ... C{0,2(W-1)}$
$C_{1,0}, C_{1,1}, C_{1,2}, ... C{1,2W-1}$
$C_{2,0}, C_{2,1}, C_{2,2}, ... C{2,2(W-1)}$
$C_{3,0}, C_{3,1}, C_{3,2}, ... C{3,2W-1}$
...
$C_{2H-1,0}, C_{2H-1,1}, C_{2H-1,2}, ... C_{2H-1,2W-1}$

1行目には1枚の障子の縦の辺数$H$,横の辺数$W$が与えられる。
2行目からの$H×2-1$行に各辺のコストCが与えられる。

出力

問題に適した回答を行うこと。
入力を促す文章などの余計な出力があった場合不正解となる。
出力の最後に改行を入れること。

制約

全ての入出力ケースについて以下を満たす。

• $1 \leq H \leq 1000$
• $1 \leq W \leq 500$
• $1 \leq C_{ij} \leq 100$
• 入力は全て整数である。

入出力例

入力例1

4 3
3 5 7 9
4 1 9 3 7
1 9 2 6
6 2 2 6 5
7 1 3 2
8 1 1 7 3
8 3 1 11

出力例1

15

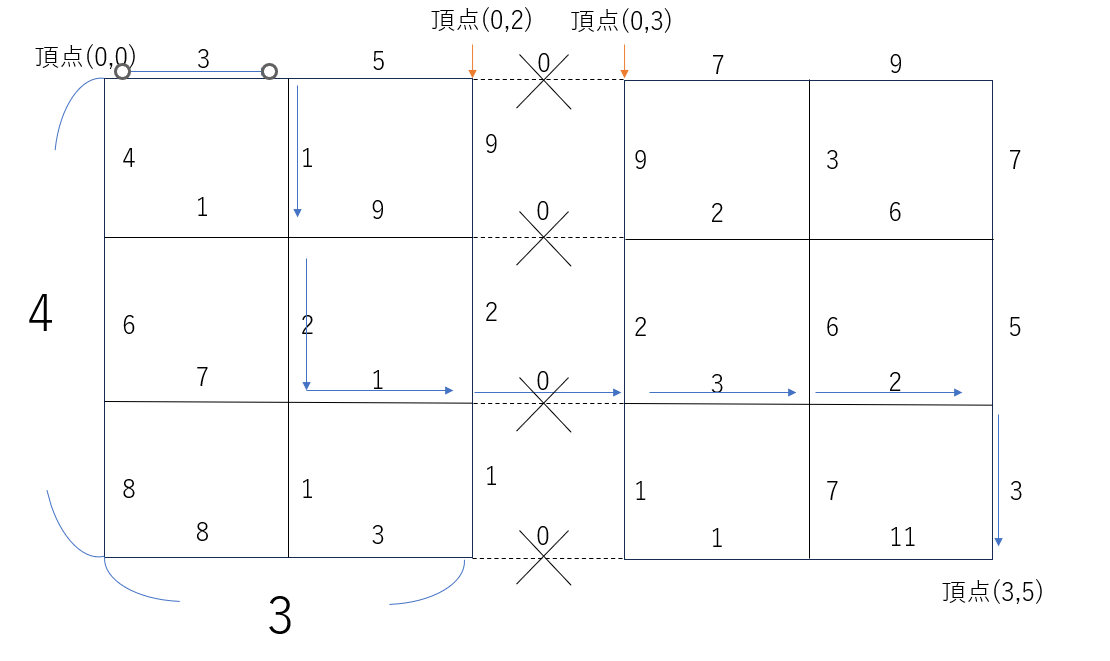
この入出力例は以下の図の通りに表せます。

閉じている状態

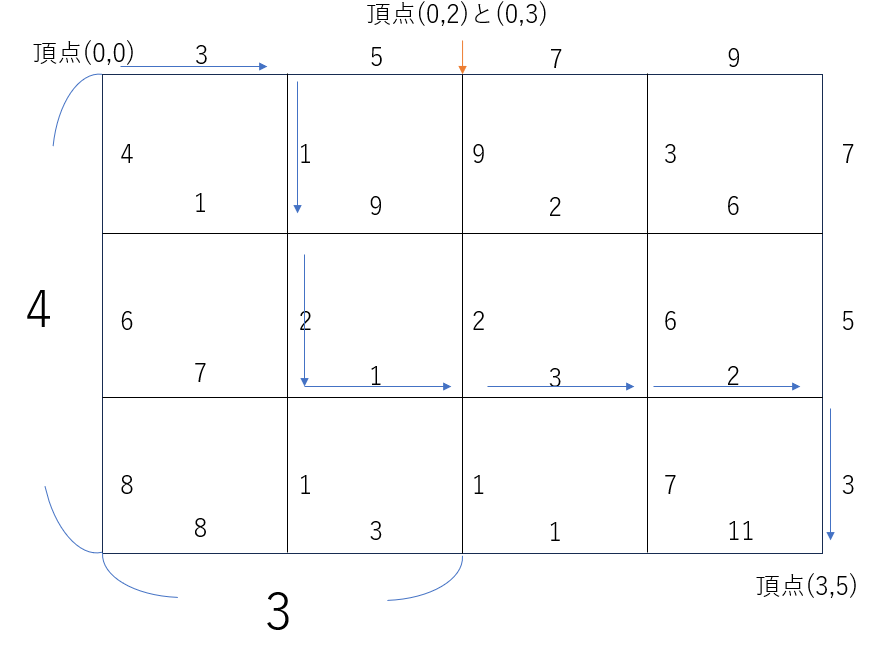
開いている状態