問題
秘境の地アイヅを探検するPCK君は、キタヤナギハラの地上絵を発見した。 キタヤナギハラの地上絵は1つの半円といくつかの線分から構成されている。
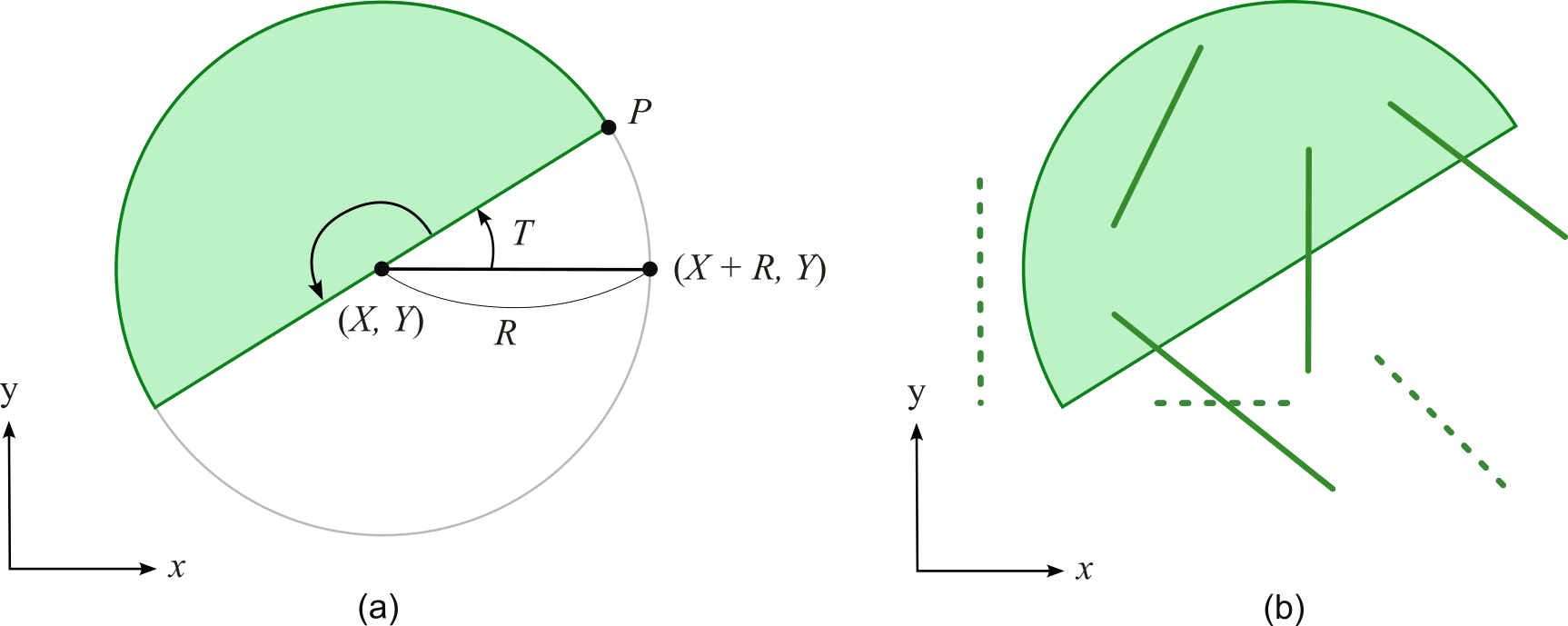
図(a)のように、半円は中心座標($X,Y$)、半径Rの円を半分にした図形である。($X + R,Y$)を($X,Y$)を中心に$T$度反時計回りに回転した点を点$P$とする。地上絵を構成する半円は、点$P$と($X,Y$)を端点とする線分を($X,Y$)を中心に反時計回りに180度回転して得られる領域(図の塗りつぶされた部分とその周囲)である。
PCK君の助手として、半円と線分の位置関係を調べてほしい。
線分の本数、半円の中心座標、半径、回転角度、線分の座標が与えられる。各線分に対して、線分の一部または全部が半円上に存在するかどうかを報告するプログラムを作成せよ。例えば、図(b)は、半円上にある4つの線分(太線)と、半円上にない3つの線分(破線)を表す。
入力
入力は以下の形式で与えられる。
$N$ $X$ $Y$ $R$ $T$ $px_1$ $py_1$ $qx_1$ $qy_1$ $px_2$ $py_2$ $qx_2$ $qy_2$ $:$ $px_N$ $py_N$ $qx_N$ $qy_N$
1行目に線分の数 $N$ ($1 \leq N \leq 100,000=10^5$) 、半円の中心座標$X,Y$ ($-1,000 \leq X,Y \leq 1,000$)、半径$R$ ($1 \leq R \leq 1,000$)、回転角度$T$ ($-180 < T \leq 180$)がすべて整数で与えられる。回転角度の単位は度で与えられる。続く$N$ 行に、$i$ 番目の線分の情報が与えられる。各行に与えられる4つの整数 $px_i,py_i,qx_i,qy_i$ ($-1,000 \leq px_i,py_i,qx_i,qy_i \leq 1,000$) は、それぞれ $i$ 番目の線分の端点の x 座標、y 座標、もう一つの端点の x 座標、y 座標を表す。ただし、入力は以下の条件を満たす。
- 線分の長さは1以上である。
- どの線分も、半円の弧とは共有点を持たない。
- 半円の弦と線分は共有点を持っても良いが、共有点を持つ場合は1点だけである。
- どの線分の端点も半円の領域の外周から0.001以上離れている。
出力
出力は$N$行である。$i$番目の線分に対して、線分の一部または全部が半円上に存在するかどうかを$i$行目に出力する。存在する場合は「 Yes 」、存在しない場合は「 No 」を出力せよ。
入出力例
入力例
2 0 0 5 0 0 -1 0 1 1 -1 2 -2
出力例
Yes No