2155 - マシュルートカ(Marshrutka)

時間制限 1 秒 / メモリ制限 512 MB / 得点 100 / Writer ei2326 / x 3 / 統計 /

TLE
1sec
MLE
512MB
得点
100

問題

ウズベキスタンは多くの観光地があるのとともに、マシュルートカという(Marshrutka)という公共交通機関が存在する。あなたはウズベキスタンに観光に来ており、多くの都市を観光したいと思っている。ここで、現実を単純化した次のような状況設定を考えたい。

ウズベキスタンには$N$個の観光地があり、$1$から$N$までの番号が付けられている。また、$M$個のマシュルートカがあり、$1$から$M$までの番号が付けられている。さらに、$S$個の交通会社があり、$1$から$S$までの番号が付けられている。$i(1 \leq i \leq M)$番のマシュルートカは観光地$U_i$から観光地$V_i$に向かって運行しており、移動には$T_i$分かかり、会社$C_i$によって管理されている。ここで、この問題では、乗り換えにかかる時間や待ち時間は発生しないものとする。
利便性のために、ウズベキスタンの各交通会社はフリーパスを発行した。交通会社$i$のフリーパスの値段はは$A_i$スムである。交通会社$i$が発光したフリーパスを持っていれば、交通会社$i$によって管理されているすべてのマシュルートカを利用することが可能になる。
さて、ウズベキスタンの観光地$1$に$1$から$Q$までの番号が付けられた$Q$人の観光客が訪れた。観光客$i$は現金$Money_i$スムを持っており、観光に使える時間は最大で$Time_i$である。
あなたの目的は、それぞれの観光客について、持っている現金の範囲内で適切にフリーパスを購入することで、観光に使える時間内に訪れることが可能な観光地の個数を最大化することである。
路線と交通会社、観光客の情報が与えられたとき、それぞれの観光客について、持っている現金の範囲内で適切にフリーパスを購入することで、観光に使える時間内に訪れることが可能な観光地の個数を最大値を求めるプログラムを作成せよ。

制約

  • $2 \leq N \leq 1000$
  • $1 \leq M \leq 3000$
  • $1 \leq S \leq 10$
  • $1 \leq A_i \leq 10^9 (1 \leq i \leq S)$
  • $1 \leq U_i,V_i \leq N (1 \leq i \leq M)$
  • $1 \leq T_i \leq 10^9 (1 \leq i \leq M)$
  • $1 \leq C_i \leq S (1 \leq i \leq M)$
  • $1 \leq Q \leq 1000$
  • $1 \leq Time_i,Money_i \leq 10^9 (1 \leq i \leq Q)$
  • 入力される値はすべて整数である。

小課題

  • 1.(4点)$S=1,Q=1$
  • 2.(2点)$S=1$
  • 3.(34点)$Q=1$
  • 4.(60点)追加の制約はない。

入力

入力は以下の形式で標準入力から与えられる。

$N$ $M$ $S$
$A_1$ $A_2$ ... $A_S$
$U_1$ $V_1$ $T_1$ $C_1$
$U_2$ $V_2$ $T_2$ $C_2$
...
$U_M$ $V_M$ $T_M$ $C_M$
$Q$
$Time_1$ $Money_1$
$Time_2$ $Money_2$
...
$Time_Q$ $Money_Q$

出力

$Q$行で出力せよ。$i$行目$(1 \leq i \leq Q)$には、観光客$i$が訪れることが可能な観光地の個数を出力せよ。 出力の最後に改行を入れること。

入出力例

入力例1

4 5 2
1 10
1 2 10 1
3 4 5 1
1 3 5 2
2 4 10 2
1 2 100 2
3
15 10
5 1
15 11

出力例1

2
1
4


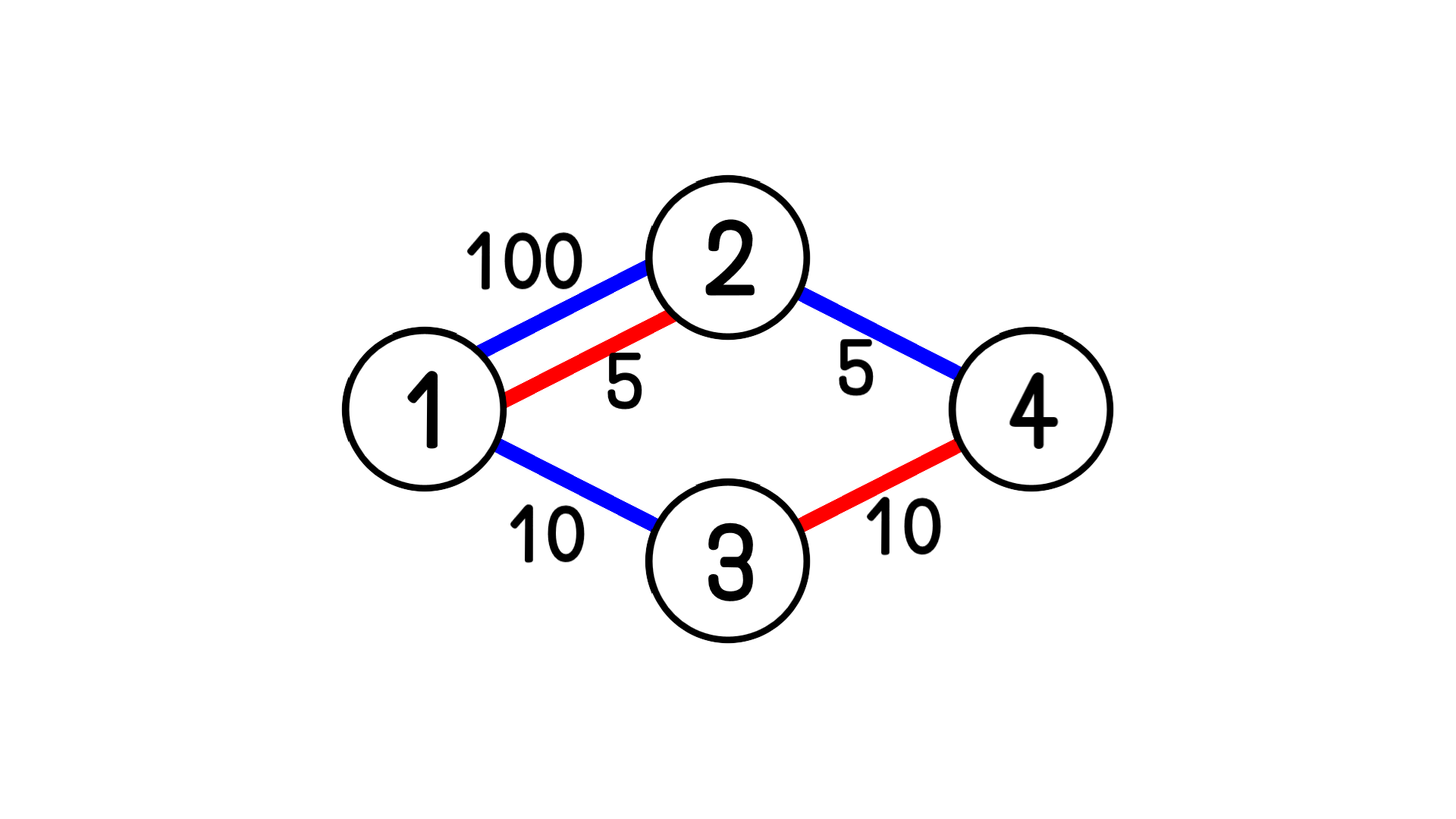
入力例1の状況設定を図で表すと上記画像のようになる。
赤線が交通会社$1$、青線が交通会社$2$によって管理されているマシュルートカである。
まず、観光客$1$は観光に最大で15分使え、10スムを持っている。10スムでフリーパスを購入する方法は、次の3通りである。
・フリーパスを購入しない。
　この場合、観光することが出来るのは観光地$1$のみである。
・交通会社$1$のフリーパスのみを購入する。
　この場合、$1$番のマシュルートカに乗ることで観光地$2$へ行くことが出来る。
　観光することが出来る観光地は$1,2$の2つである。
・交通会社$2$のフリーパスのみを購入する。
　この場合、$3$番のマシュルートカに乗ることで観光地$3$へ行くことが出来る。
　観光することが出来る観光地は$1,3$の2つである。
適切にフリーパスを購入することで、2つの観光地に行くことが出来る。また、3つ以上の観光地へ行くことはできないため、2を出力する。
次に、観光客$2$はどのフリーパスを購入することもできない。よって、訪れることが出来るのは観光地$1$のみなので、1を出力する。
また、観光客$3$はすべてのフリーパスを購入することができ、15分であればどの観光地へも行くことが可能である。よって4を出力する。
この入力例は小課題$4$を満たす。

入力例2

5 7 4
9 4 8 11
1 2 5 4
2 5 7 3
4 3 8 1
5 4 12 2
1 1 3 1
3 2 4 4
5 3 19 2
4
31 15
29 18
16 11
64 73

出力例2

4
4
3
5
この入力例は小課題$4$を満たす。

入力例3

3 2 1
5
1 2 1 1
2 3 1 1
1
1 5

出力例2

2
この入力例は小課題$1,2,3,4$を満たす。

入力例4

4 5 1
1000000000
1 2 5 1
2 4 9 1
1 3 4 1
3 4 2 1
1 4 19 1
5
100 1
3 1000000000
5 1000000000
7 1000000000
8 1000000000

出力例2

1
1
3
4
4
この入力例は小課題$2,4$を満たす。