問題
太郎君の住んでいるJOI市は,南北方向にまっすぐに伸びる a 本の道路と,東西方向にまっすぐに伸びる b 本の道路により,碁盤の目の形に区分けされている.南北方向の a 本の道路には,西から順に 1, 2, ... , a の番号が付けられている.また,東西方向の b 本の道路には,南から順に 1, 2, ... , b の番号が付けられている.西から i 番目の南北方向の道路と,南から j 番目の東西方向の道路が交わる交差点を (i, j) で表す.
太郎君は,交差点 (1, 1) の近くに住んでおり,交差点 (a, b) の近くのJOI高校に自転車で通っている.自転車は道路に沿ってのみ移動することができる.太郎君は,通学時間を短くするため,東または北にのみ向かって移動して通学している.
現在, JOI市では, n 個の交差点 (x1, y1), (x2, y2), ... , (xn, yn) で工事を行っている.太郎君は工事中の交差点を通ることができない.
太郎君が交差点 (1, 1) から交差点 (a, b) まで,工事中の交差点を避けながら,東または北にのみ向かって移動して通学する方法は何通りあるだろうか.太郎君の通学経路の個数 m を 10007 で割ったあまりで求めよ.
入力
1行目には空白を区切りとして2個の整数 a, b が書かれている.これは,南北方向の道路の本数と,東西方向の道路の本数を表す. a, b は 1 ≤ a, b ≤ 1000 をみたす.
2行目には, 工事中の交差点の個数を表す整数 n が書かれている. n は 0 ≤ n ≤ 40 をみたす.
続く n 行 (3行目から n+2 行目) には,工事中の交差点の位置が書かれている. i+2 行目には空白で区切られた整数 xi, yi が書かれており,交差点 (xi, yi) が工事中であることを表す. xi, yi は 1 ≤ xi, yi ≤ 16 をみたす.
出力
太郎君の通学経路の個数 m を 10007 で割った余りのみからなる1行である.
入出力例
入力例1
5 4 3 2 2 2 3 4 2
出力例1
5
入力例1は以下の図に対応している。
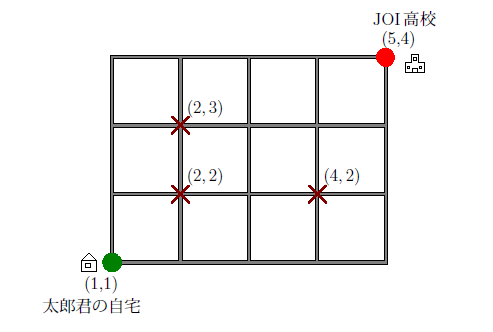
この場合,通学経路は m=5 通りある. 5通りの通学経路を全て図示すると,以下の通り.
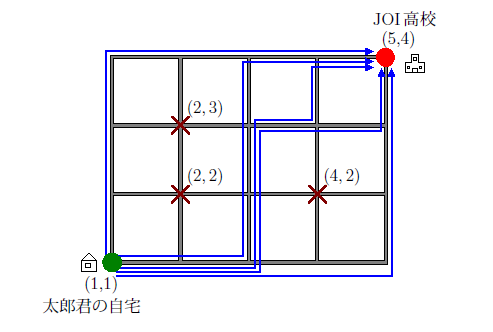
入力例2
20 20 0
出力例2
9429
工事地点がない場合もあり得る。
985525432 通りあるので、これを 10007 で割った余り 9429 を出力する。
入力例3
1000 1000 3 10 10 20 20 30 30
出力例3
3772