問題
JOI 町に住む太郎君は, ある日, 健康増進のために散歩を日課にしようと思い立った. 太郎君の住む JOI 町には, 図のように, 東西方向に走る (H + 1) 本の道路と, 南北方向に走る (W + 1) 本の道路が碁盤目状に通っている. 太郎君の家はもっとも北西の交差点にあり, ここから散歩を開始する.
以降, 北から a 番目, 西から b 番目の交差点を (a, b) で表す. たとえば, 太郎君の家がある交差点は (1, 1) である.
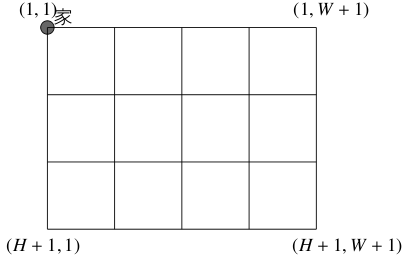
図: JOI 町の図 (H = 3, W = 4 の場合). 図の上が北, 左が西に対応する.
太郎君は, 散歩のルートが日々違ったほうが面白いと考えたので, (1, 1) から (H, W) までの H × W 個の交差点に, 「東」または「南」の文字を書き, 次のようなルールに従って毎日散歩を行うことにした.
- 文字の書かれた交差点にいる場合, その交差点に書かれている文字が「東」な ら「南」に, 「南」なら「東」に文字を書き換え, もともと書かれていた文字の方角にある次の交差点まで進む.
- もっとも東やもっとも南の道路に到達したら散歩を終了する.
この計画を考えた後, 太郎君は, 将来の散歩で自分がどのようなルートをたどることになるのかが気になった. 太郎君のために, 太郎君の N 回目の散歩のルートを予測するプログラムを作成せよ.
入力
標準入力から以下の入力を読み込め.
- 1 行目には, 3 つの正整数が空白区切りで書かれている. これらは, 問題文中の 3 つ の数値 H, W, N の値である. H, W, N はそれぞれ, 1 ≤ H ≤ 1000, 1 ≤ W ≤ 1000, 1 ≤ N ≤ 10000000 = 107 をみたす.
- 2 行目から H + 1 行目には, それぞれ W 個の整数が空白区切りで書かれている. これらは, 太郎君が最初に交差点に書いた文字の情報を表す. i + 1 行目の j 番目の整数が 0 なら, 交差点 (i, j) に書かれた文字が「南」であることを, 1 なら, 交差点 (i, j) に書かれた文字が「東」であることを表す.
採点用データのうち, 配点の 30% 分については, H ≤ 100, W ≤ 100, N ≤ 1000 を満たす.
出力
N 回目の散歩において太郎君が散歩を終了する交差点が (i, j) のとき, i と j をこの順に空白で区切って出力せよ.
入出力例
入力例 1
3 4 3 1 0 1 1 0 1 0 0 1 0 1 0
出力例 1
1 5
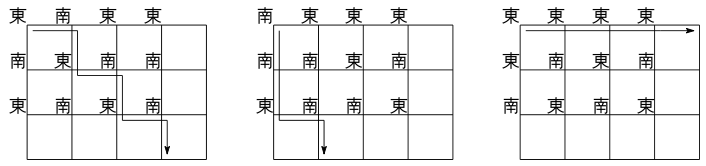
上の例では, 1 回目から 3 回目の散歩のルートは次の図のようになる.