0360 - 宇宙海賊 (Space Pirate)

問題

　宇宙の遥か彼方，とある銀河には，文明が発達した N 個の星がある．星には 1 から N までの番号がついている．それぞれの星には 1 台のテレポーターがあり，それぞれのテレポーターには行き先の星が定まっている．テレポーターは一方通行である．
　この銀河では銀河帝国美術館が星々を回って美術展を開いている．美術展は現在，星 1 で開催されている．次の美術展が開催される星は，星 1 からテレポーターで K 回移動した先であることが決まっている．宇宙警察は，宇宙海賊がこの美術館の美術品を狙っていることを突き止めた．宇宙警察の調査によると，宇宙海賊は，ある星 a のテレポーターの行き先をクラッキングによって星 b に不正に上書きすることで，次の美術展が開催される星を変更しようと目論んでいる．宇宙海賊がクラッキングを行う星は 1 つのみである．しかし，a, b の値が具体的に何であるかは分からなかった．
　宇宙警察は，美術展の行き先を予測するために，それぞれの星 i について，次の美術展が星 i で開催されるような組 (a, b) の個数を知りたい．この計算は複雑なので，優秀なプログラマーであるあなたに計算を依頼することになった．

課題

　テレポーターの現在の行き先が与えられたとき，それぞれの星 i について，次の美術展が星 i で開催されるような組 (a, b) の個数を計算するプログラムを作成せよ．

入力

　標準入力から以下の入力を読み込め．

• 1 行目には，2 つの整数 N, K が空白を区切りとして書かれている．これは，星が N 個あり，次の美術展を開く場所を決めるためにテレポーターで移動する回数が K であることを表す．
• 続く N 行のうちの i 行目 (1 ≤ i ≤ N) には，整数 A_i (1 ≤ A_i ≤ N) が書かれている．これは，星 i のテレポーターの現在の行き先が A_i であることを表す．

出力

　標準出力に N 行で出力せよ．i 行目 (1 ≤ i ≤ N) に，次の美術展が星 i で開催されるような組 (a, b) の個数を出力せよ．

注意

• 星 i のテレポーターの行き先が星 i 自身となることもあり得る．この場合，星 i から何回テレポーターで移動しても，星 i にとどまり続ける．
• 星 a のテレポーターの現在の行き先が星 b であるにも関わらず，宇宙海賊がクラッキングにより星 a のテレポーターの行き先を星 b に上書きすることがあるかもしれない．この場合，上書きによって，星 a のテレポーターの行き先は変化しない．このような組 (a, b) も含めて数えること．

制限

　すべての入力データは以下の条件を満たす.

• 1 ≤ N ≤ 100 000．
• N ≤ K ≤ 10¹⁸．

小課題

小課題 1 [10 点]

• N ≤ 100 を満たす．

小課題 2 [37 点]

• N ≤ 3 000 を満たす．

小課題 3 [33 点]

• A_i ≠ A_j (1 ≤ i < j ≤ N)．

小課題 4 [20 点]

　追加の制限はない．

入出力例

入力例 1

5 7
5
1
4
3
2

出力例 1

1
2
3
3
16

　この入力例において，それぞれのテレポーターの現在の行き先は図 1 のようになる．

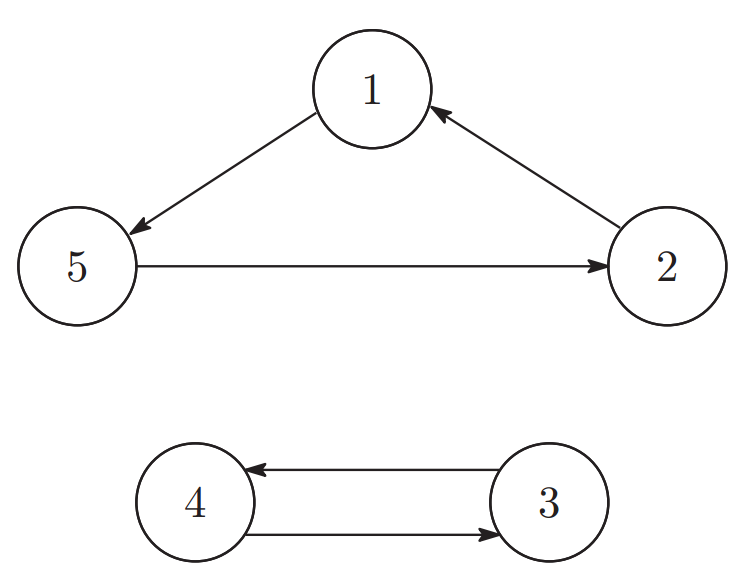
図 1

　(a, b) = (1, 4) の場合，星 1 のテレポーターの行き先がクラッキングにより星 4 に上書きされる．テレポーターの行き先は図 2 のようになる．このとき，星 1 からテレポーターで 7 回移動した先は星 4 なので，次の美術展は星 4 で開催される．（テレポーターにより 1 → 4 → 3 → 4 → 3 → 4 → 3 → 4 と移動する．）

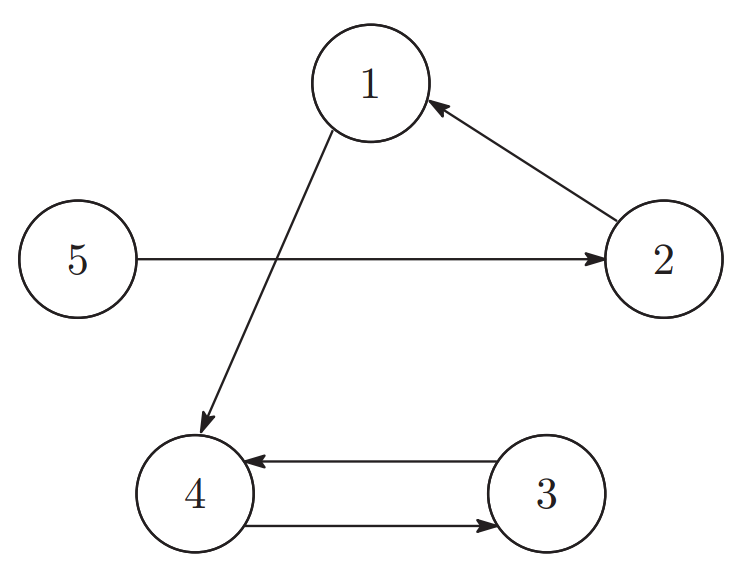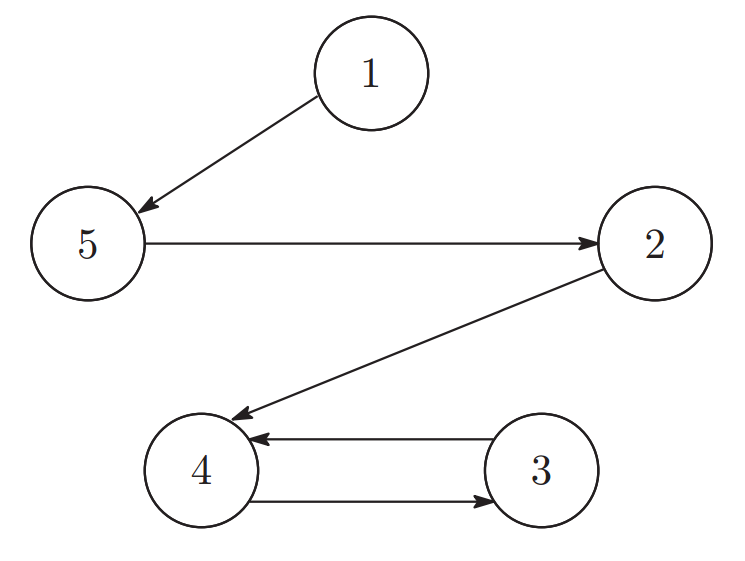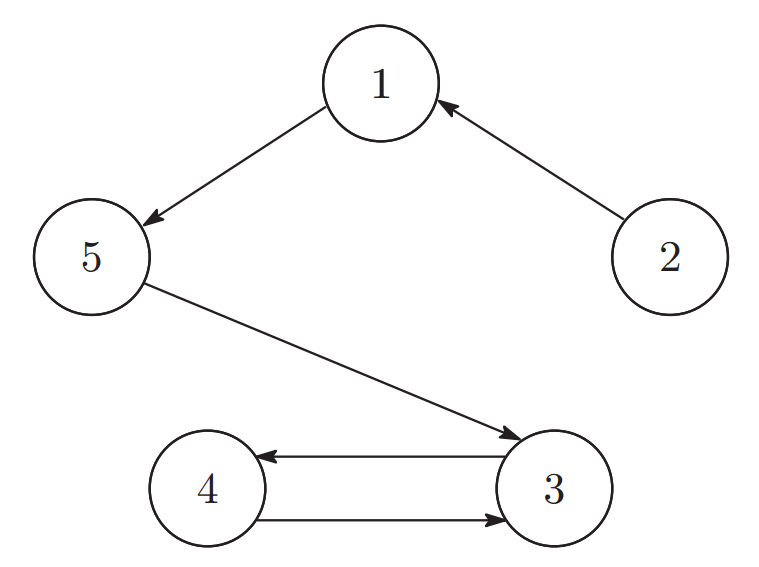図 2	図 3	図 4

　次の美術展が星 4 で開催される組 (a, b) は，全部で (1, 4), (2, 4), (5, 3) の 3 個ある．
　この入力例において，次の美術展が星 i で開催される組 (a, b) をまとめると以下の表のようになる．

i	次の美術展が星 i で開催されるような組 (a, b)
1	(1, 1)
2	(1, 2), (2, 2)
3	(1, 3), (2, 3), (5, 4)
4	(1, 4), (2, 4), (5, 3)
5	(1, 5), (2, 1), (2, 5), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 5)

　a = b の場合や，上書きしても星 a のテレポーターの行き先が変化しない場合も含めて数える必要があることに注意せよ．

入力例 2

40 57
9
24
1
28
29
5
9
1
36
5
35
14
14
29
28
34
28
4
34
36
33
11
22
23
10
18
26
33
36
15
37
31
27
16
25
37
6
31
21
31

出力例 2

4
2
1
12
18
9
1
1
15
0
4
0
0
2
0
11
0
12
0
2
0
0
1
0
5
12
13
13
34
0
5
1
15
10
8
1351
36
1
0
1