0361 - ピンボール (Pinball)

時間制限 1 秒 / メモリ制限 512 MB / 得点 100 / Writer root / x 2 / 統計 /

TLE
1sec
MLE
512MB
得点
100

問題

　アリスはピンボールというテレビゲームが好きである．ピンボールとは以下のようなゲームである．
　盤 と呼ばれる (M + 2) 行 N 列のマス目がある．盤の 1 行目を 最上部，(M + 2) 行目を 最下部 と呼ぶことにする．また，盤の i 行 j 列目を (i, j) で表すことにする．
　盤の最上部のどこかの列にボールが現れ，最下部に向かって盤の行と垂直に落ちていく．すなわち，最上部の (1, i) (1 ≤ i ≤ N) にボールが現れ，(j, i) (2 ≤ j ≤ M + 1) を通り，最下部の (M + 2, i) に到達する．最下部に到達したボールをうまく打ち返すことで アリスの得点となる．
　アリスは，このままでは最下部のあらゆる列にボールが到達する可能性があるため，打ち返すのが困難だと気がついた．そこで アリスは，以下のような装置のうちいくつかをうまく配置することで，最下部でボールが到達する可能性があるマスを 1 つにしようと考えた．
　使用できる装置が M 個あり，装置には 1 から M までの番号が付いている．どの装置も盤の行と平行であり，装置 i (1 ≤ i ≤ M) はマス (i + 1, Ai) から (i + 1, Bi) までの (Bi - Ai + 1) マスを占める (1 ≤ Ai ≤ Bi ≤ N)．この装置のどこかにボールが到達すると，ボールは (i + 1, Ci) (Ai ≤ Ci ≤ Bi) に移動する．移動したボールは再び，盤の Ci 列目を盤の行と垂直に落ち始める．同じ装置がひとつのボールに 2 回以上作用することはない．
　ただし，装置 i (1 ≤ i ≤ M) を設置するためにはゲーム内で Di 円の費用が必要である．M 個の装置のうち設置するものをうまく選ぶことで，最下部でボールが到達する可能性があるマスの数を 1 つにし，かつ費用の合計をできるだけ小さくしたい．


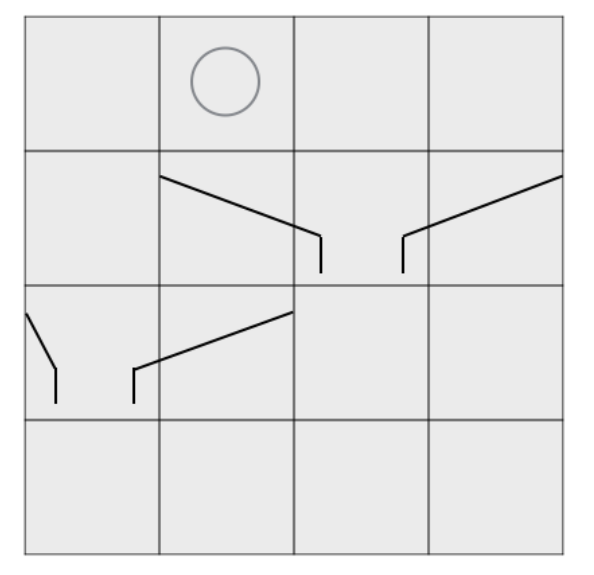
図：ピンボールの例．M = 2，N = 4 である．ボールはいま最上部の (1, 2) に現れている．この後ボールは (2, 2) に落ちたのち，装置 1 により (2, 3) に移動し，最終的に最下部の (4, 3) に到達する．

課題

　盤の大きさと装置の情報が与えられる．最下部でボールが到達する可能性があるマスの数が 1 つになるように装置を設置した場合の，装置の費用の合計の最小値を求めるプログラムを作成せよ．

入力

　標準入力から以下のデータを読み込め．

  • 1 行目には整数 M, N が空白を区切りとして書かれている．これは，盤が (M + 2) 行 N 列であり，装置が M 個存在することを表す．
  • 続く M 行のうち i 行目 (1 ≤ i ≤ M) には 4 つの整数 Ai, Bi, Ci, Di が空白を区切りとして書かれている．これは，装置 i が (i + 1, Ai) から (i + 1, Bi) までの (Bi - Ai + 1) マスを占め，これらのマスに到達したボールが (i + 1, Ci) に移動することと，装置 i を設置するための費用が Di 円であることを表す．

出力

　最下部でボールが到達する可能性があるマスの数が 1 つになるように装置を設置した場合の，装置の費用の合計の最小値を，円単位で標準出力に 1 行で出力せよ．そのように装置を設置することが不可能な場合，-1 を出力せよ．

制限

　すべての入力データは以下の条件を満たす.

  • 1 ≤ M ≤ 100 000.
  • 2 ≤ N ≤ 1 000 000 000．
  • 1 ≤ Ai ≤ Ci ≤ Bi ≤ N (1 ≤ i ≤ M).
  • 1 ≤ Di ≤ 1 000 000 000 (1 ≤ i ≤ M).

小課題

小課題 1 [11 点]

　以下の条件を満たす．

  • M ≤ 10．
  • N ≤ 1 000．

小課題 2 [18 点]

　以下の条件を満たす．

  • M ≤ 200.

小課題 3 [22 点]

　以下の条件を満たす．

  • M ≤ 1000.

小課題 4 [49 点]

　追加の制限はない．

入出力例

入力例 1

5 6
2 4 3 5
1 2 2 8
3 6 5 2
4 6 4 7
2 4 3 10

出力例 1

25

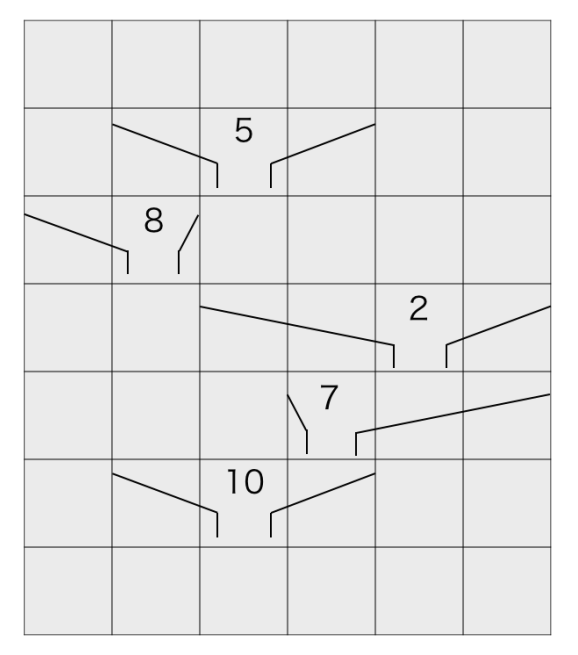
　この入力例において，盤と装置の状態は下図のようになる．装置の上の数字はその装置を設置するのに必要な費用（単位は円）を表す．

　5 つの装置のうち，装置 2・4・5 を設置すると下図のようになる．

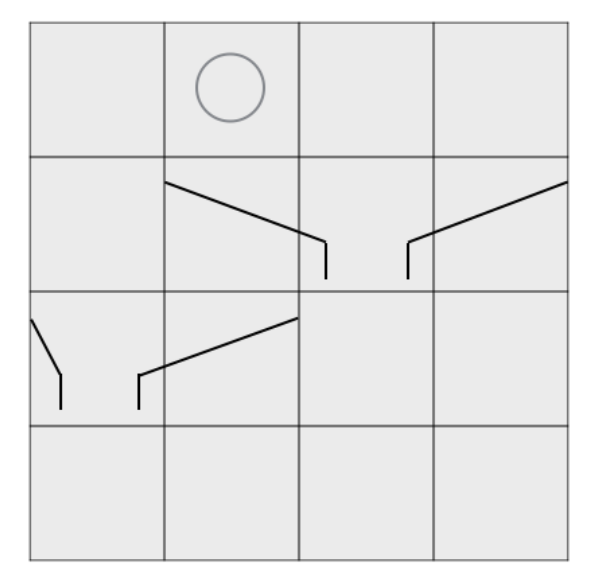
　このとき，最上部のどの列にボールが現れても最下部の (7, 3) にボールが到達する．このときの装置の費用の合計は 25 円となる．費用の合計が 25 円未満で最下部でボールが到達する可能性があるマスの数が 1 つになるように装置を設置することはできないため，25 を出力する．

入力例 2

3 5
2 4 3 10
1 3 1 20
2 5 4 30

出力例 2

-1

　この入力例では，最下部でボールが到達する可能性があるマスの数が 1 つになるように装置を設置することはできない．