Problem Statement
あなたは親友であるみさわさんの誕生日が近いことに気づき,根付きの二分木をプレゼントすることにした. ここで,根付きの二分木とは,以下のようなグラフ構造である.(図 1)
- 各頂点には,その頂点の親と呼ばれる頂点がちょうど 1 つだけ存在し,親と辺で結ばれている.ただし,根と呼ばれる 1 つの頂点のみ,例外的に親を持たない.
- 各頂点は,左の子と呼ばれる頂点をちょうど 1 つ持つか,あるいは持たない.左の子を持つ場合,左の子とは辺で結ばれており,左の子の親はその頂点である.
- 各頂点は,右の子と呼ばれる頂点をちょうど 1 つ持つか,あるいは持たない.右の子を持つ場合,右の子とは辺で結ばれており,右の子の親はその頂点である.
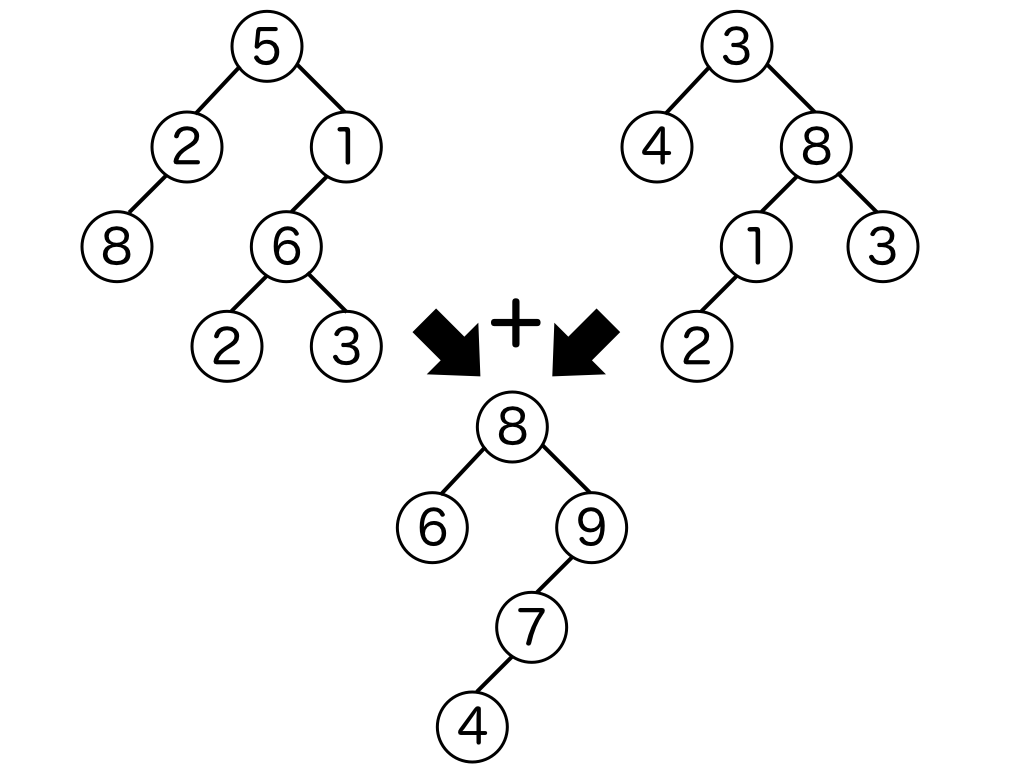
図 1. 2 つの根付きの二分木とその合成の例
あなたは手作りの品を贈りたいと考えたので,市販の根付きの二分木を 2 つ買ってきて重ね合わせて合成することで,さらによい根付きの二分木を 1 つ作ることにした. あなたが買ってきた 2 つの木の各頂点には非負の整数が書かれている. みさわさんは少ない頂点数で各数値が大きいような,コストパフォーマンスがよい木が好みなので,以下の手順に沿って新しい二分木を作ることにする.
- 2 つの二分木それぞれの根に書かれた整数の和を,新しい二分木の根に書く整数とする.
- どちらの二分木の根も左の子を持っている場合,それらを根とする二分木それぞれを合成した二分木を作り,新しい二分木の根の左の子とする.そうでない場合,新しい二分木の根は左の子を持たない.
- どちらの二分木の根も右の子を持っている場合,それらを根とする二分木それぞれを合成した二分木を作り,新しい二分木の根の右の子とする.そうでない場合,新しい二分木の根は右の子を持たない.
あなたは実際に合成する作業を行う前に,できあがる根付きの二分木がどのようになるのか確かめることにした. 買ってきた 2 つの根付きの二分木の情報が与えられるので,上記の手順に従って合成される新しい根付きの二分木を求めるプログラムを作成せよ.
ここで,根付きの二分木の情報は以下のような形式で文字列として表現するものとする.
(左の子を表す文字列)[根に書かれた整数](右の子を表す文字列)
節点が存在しない木は空文字列とする.例えば図 1 の合成されてできた新しい根付きの二分木は '(()[6]())[8](((()[4]())[7]())[9]())' のように書く.
Input
入力は次の形式で表される.
A B
A,B はそれぞれ買ってきた根付きの二分木の情報を表す文字列であり,長さは 7 以上 1 000 以下である. 与えられる情報は前述の形式に従っており,余計な空白文字等を含まない. また,節点が存在しない根付き木が入力されることはない. 各節点に書かれた整数は 0 以上 1 000 以下であると仮定してよい. ただし,出力の各節点に書かれる整数はこの範囲に収まらない場合もあることに注意せよ.
Output
2 つの根付きの二分木を合成してできあがる新しい根付きの二分木の情報を 1 行で出力せよ.特に,行末の改行を除く余計な空白文字等を含まないよう注意せよ.
Sample Input 1
((()[8]())[2]())[5](((()[2]())[6](()[3]()))[1]()) (()[4]())[3](((()[2]())[1]())[8](()[3]()))
Output for the Sample Input 1
(()[6]())[8](((()[4]())[7]())[9]())
Sample Input 2
(()[1]())[2](()[3]()) (()[1](()[2]()))[3]()
Output for the Sample Input 2
(()[2]())[5]()
Sample Input 3
(()[1]())[111]() ()[999](()[9]())
Output for the Sample Input 3
()[1110]()
Sample Input 4
(()[2](()[4]()))[8]((()[16]())[32](()[64]())) ((()[1]())[3]())[9](()[27](()[81]()))
Output for the Sample Input 4
(()[5]())[17](()[59](()[145]()))
Sample Input 5
()[0]() ()[1000]()
Output for the Sample Input 5
()[1000]()