0450 - ワープ航法

飛行時間を大幅に短縮するワープ航法は空の旅を変革しつつある．航空機は，地表面に設置したワープ場の上に到達しさえすれば，好きな行き先に瞬く間に移動できるのだ．

残念ながらこの分野の現在の未熟な技術ではワープ場の設置はとても高価につく． 予算が許す範囲では 2 箇所にしか設けられない． 幸いにしてワープ場のコストは設置場所に依存しないので，地表面のどこにでもワープ場を設置してもよい．空港に設置することさえできる．

あなたの仕事は，空港の位置とその間の片道航空便の一覧をもとに，平均コストを最小にできる 2 箇所のワープ場の設置場所をみつけることだ． 平均コストとは，全航空便の飛行時間の二乗平均平方根，すなわち以下で与えられる．

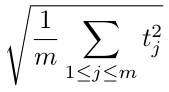
ここで，m は航空便の総数，t_j は j 番目の便の最短飛行時間である． t_j の値はワープ場の設置場所に依存することに注意せよ．

簡単のため，地表面は平坦な二次元平面で，空港，航空機，ワープ場はその平面上の点で近似するものとする． 航空便が使う航空機の巡航速度は異なり得る． 航空機の上昇，加速，減速，降下に要する時間は無視できる． また，ワープ場に到達した航空機がそこから行き先に移動するのに掛かる時間はゼロである． 後述するように，空港の座標はすべて整数で与えられるが，ワープ場の座標は非整数値を取りうることに注意せよ．

入力は 35 個以下のデータセットからなる．各データセットは次の形式で表される．

n m
x1 y1
...
xn yn
a1 b1 v1
...
am bm vm

n は空港の数，m は航空便の数を表す(2 ≤ n ≤ 20, 2 ≤ m ≤ 40)． 各 i について，(x_i, y_i) は i 番目の空港の座標を表す． それぞれの座標値 x_i, y_i は整数であり，その絶対値は 1000 を超えない． 各 j について，a_j と b_j は 1 から n までの整数で，それぞれ j 番目の航空便の出発空港と到着空港の番号を表す． また，v_j は j 番目の航空便の航空機の巡航速度，すなわち単位時間あたりの移動距離を表す． v_j は十進小数であり，小数第二位まで与えられる (1 ≤ v_j ≤ 10)．

以下のことが保証されている．

• 異なる空港は異なる座標を持つ．
• すべての航空便で，出発空港と到着空港は異なる．
• 異なる航空便は出発空港と到着空港の少なくとも一方が異なる．

入力の終わりは，2つのゼロからなる行で表される．

各データセットについて，2 箇所のワープ場を最適に設置した場合の平均コストを出力せよ．出力には 10^-6 を超える絶対誤差があってはならない．

3 4
100 4
100 0
0 0
1 2 1.00
2 1 1.00
3 1 9.99
3 2 9.99
7 6
0 0
1 0
2 0
0 10
1 10
2 10
20 5
1 7 1.00
2 7 1.00
3 7 1.00
4 7 1.00
5 7 1.00
6 7 1.00
4 4
-1 -1
1 -1
-1 1
1 1
1 4 1.10
4 2 2.10
2 3 3.10
3 1 4.10
8 12
-91 0
-62 0
-18 0
2 0
23 0
55 0
63 0
80 0
2 7 3.96
3 2 2.25
2 4 5.48
8 7 9.74
5 6 6.70
7 6 1.51
4 1 7.41
5 8 1.11
6 3 2.98
3 4 2.75
1 8 5.89
4 5 5.37
0 0

1.414214
0.816497
0.356001
5.854704