問題
円環上に N 個の足場が等間隔に並んでいます. それぞれの足場は隣接する足場と距離 1 ずつ離れています. 足場には 1 から N までの番号が順番につけられていて, 足場 1 と N は隣接しています.
あなたは突然ぴょんしたくなりました.
今, あなたは足場 1 にいます. あなたは 1 回ぴょんすると, 円環上を滑空して他の足場に移動できます. しかし, ちょっと不器用なので, 距離が D 離れた足場にしか移動できません.
あなたは無限にぴょんしていたいのですが, 足場はデリケートです. 1 度ぴょんすると, もともといた足場は消えてしまいます.
最大で何回ぴょんできるか求めてください.
入力
N D
1 行に円環の足場の数 N と, ぴょんする距離 D が半角空白区切りで与えられる.
制約
すべての入出力例は以下の制約を満たす.
- 2 ≤ N ≤ 1 000 000 000 (= 109)
- 0 ≤ D ≤ N
出力
ぴょんできる最大の回数を出力せよ.
入出力例
入力例 1
4 2
出力例 1
1
例えば以下の図のようにぴょんします.
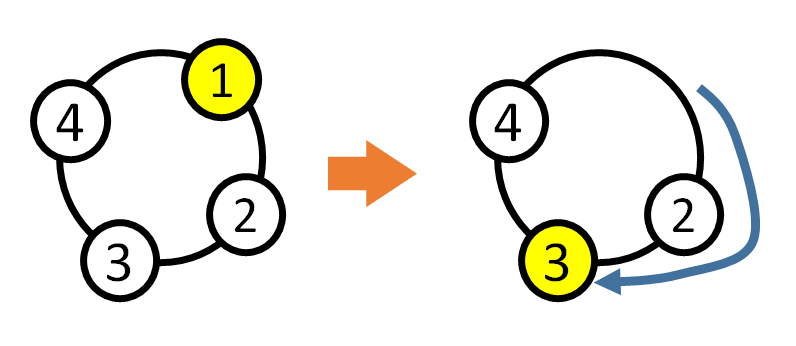
入力例 2
5 2
出力例 2
4
例えば以下の図のようにぴょんします.
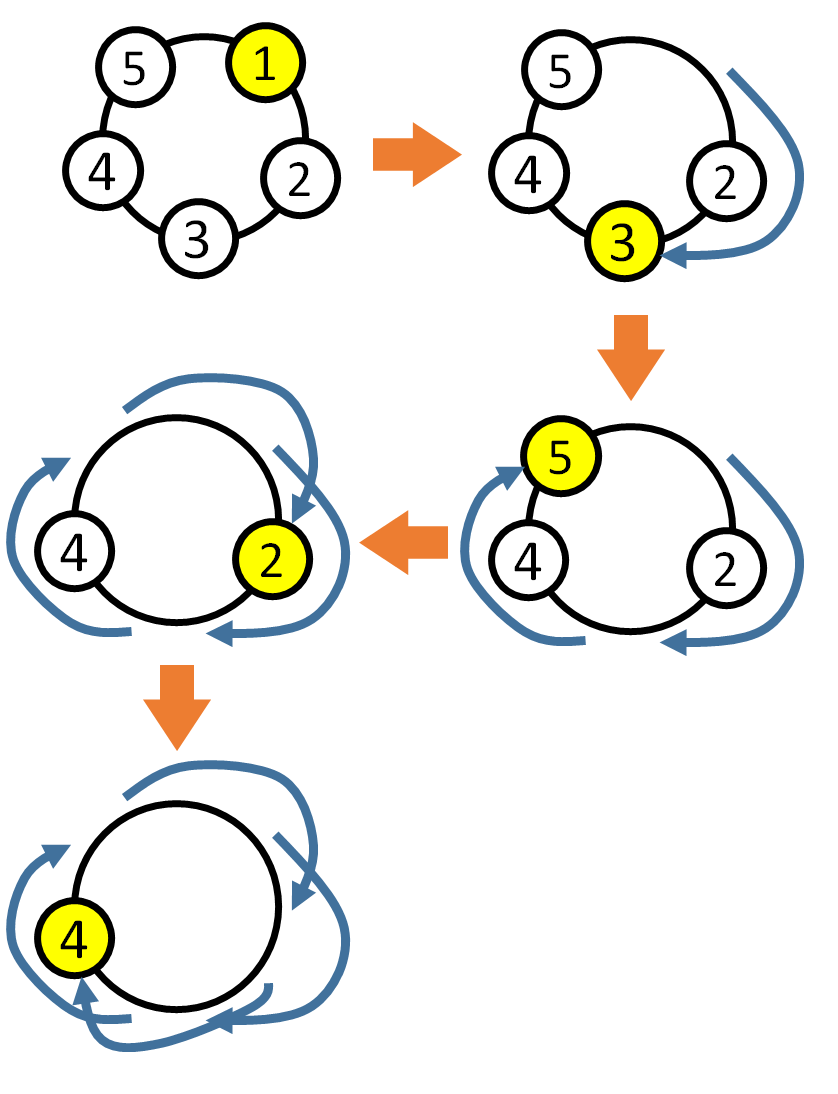
入力例 3
10 10
出力例 3
0
一度もぴょんできない場合があることに注意してください.
コメント
簡単だけど難しい...