ストーリー兼問題
????天皇「東京ってまぢ人多くなぁーい??」
上記の一言で日本の首都が移転することになった.
どうやら新しい日本の首都は日本のちょうど真ん中辺りに位置する浜松になるようだ.
首都移転に伴って浜松は駅数V駅,線路数E本の大都市になる計画だ.
そして,これから発展していく浜松に目をつけたN社の企業がいくつかの路線を開通させる予定である.
N社はそれぞれ1~Nの番号が付けられており,企業競争の末N社全てで次のサービスを実行する事となった.
「Ni社の社長の知り合いの, 知り合いの, 知り合い...の, 知り合いがあなたならば運賃を半額にする.」
つまりNi社の社長の知り合いを辿っていった際,最終的にあなたに辿り着くならばNi社が敷いた路線の運賃はどの線路も半額になる.
ただし,元の運賃が奇数の場合は運賃/2の小数部を切り捨てたものを半額とする.
社長はそれぞれ企業番号と対応した1~Nで表される.
あなたは0で表され,その他の知り合いはNより大きい整数で表される.
あなたがS駅からG駅へ行きたい場合,最小いくらあればたどり着けるかを調べて欲しい.
もしS駅からG駅へ行く経路が無いときはNAを出力せよ.
ただし,浜松はただいま絶賛発展途上中なので計画のE本より線路数が増える可能性がある.
更に,言うまでもないが知り合いは時間と共に徐々に変化していく事もあなたは考慮しなければならない.
入力
V E N a1 b1 c1 d1 . . . . . . . . . . . . aE bE cE dE Q 0 a b c d 1 p q 2 S G . . .
1行目に整数V, E, Nが与えられる. これはそれぞれ駅数, 線路数, 企業数を表す.
その後,E+1行にわたりai, bi, ci, diの4つの整数が与えられる.
これはai, bi間の運賃がci円であり,この線路がdi社の路線であることを表す.
E+2行目にクエリの回数Qが与えられる.
その後,Q行にわたり,以下の情報が入力される.
- 先頭の入力が0の場合はa, b, c, dが続けて与えられる.
これはa, b間の線路が新たに増え,その運賃がc円であり,d社の路線であることを表す. - 先頭の入力が1の場合はp, qが続けて与えられる.
これは人pと人qが新たに知り合いになったことを表す.
- 先頭の入力が2の場合はS, Gが続けて与えられる.
これはS駅を出発し,G駅に到着するときの最小運賃を求め,出力しなければならない事を表す.
出力
先頭の入力が2のクエリが与えられた時S駅からG駅に行くときの最小運賃を出力せよ.
もしS駅からG駅へ行く経路が無いときはNAを出力せよ.
出力毎に改行を入れること.
制約
全ての入出力ケースは整数であり,以下を満たす。
- 1 ≦ a, b, S, G ≦ V, c ≦ 1000(= 103)
- 1 ≦ d ≦ N ≦ E, Q ≦ 10000(= 104)
- 0 ≦ p, q ≦ 1000000(= 106) ※なお,クエリの先頭の入力が2である量はQの1%程度である.
入出力例
入力例
9 13 3 1 2 2 1 2 3 5 1 2 3 6 2 1 4 1 3 2 4 1 1 2 5 2 1 3 5 4 3 3 8 3 2 5 8 4 3 5 8 3 2 4 5 6 3 4 7 3 1 4 6 2 2 11 2 1 8 2 3 7 0 7 8 2 1 2 1 8 2 3 7 1 4 1 1 4 9 1 9 0 2 1 8 2 3 7 2 1 9
出力例
7 9 6 5 3 3 NA
解説
最初の入力を図で表すと以下のようになる.
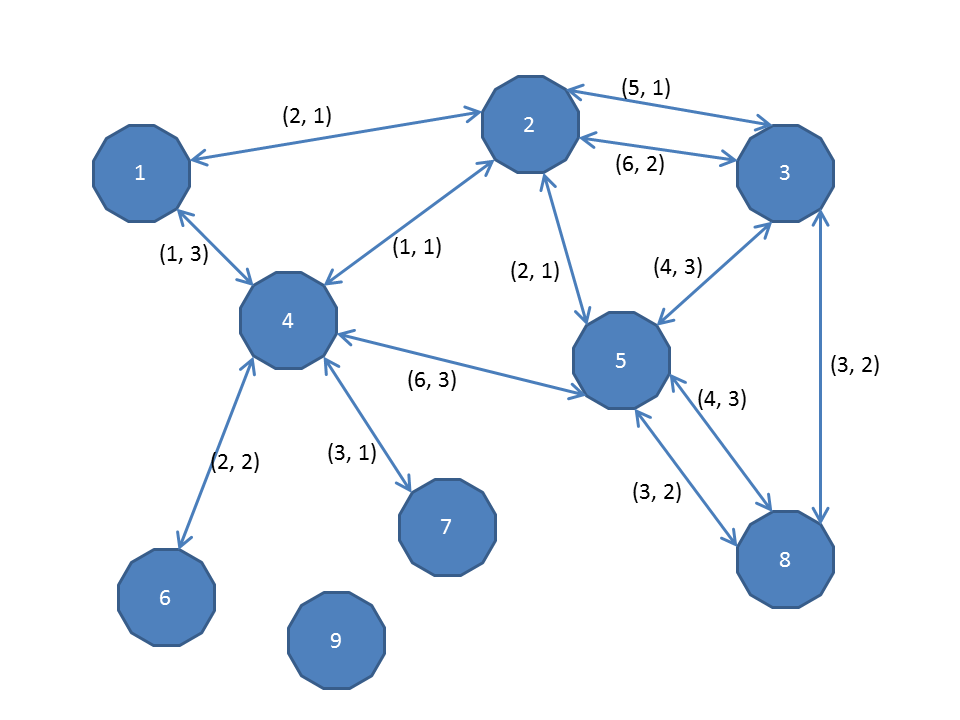
この時1-8, 3-7間のそれぞれの最小運賃は7, 9となる.
次に7-8間へ行く線路がつながった時の図は以下のようになる.
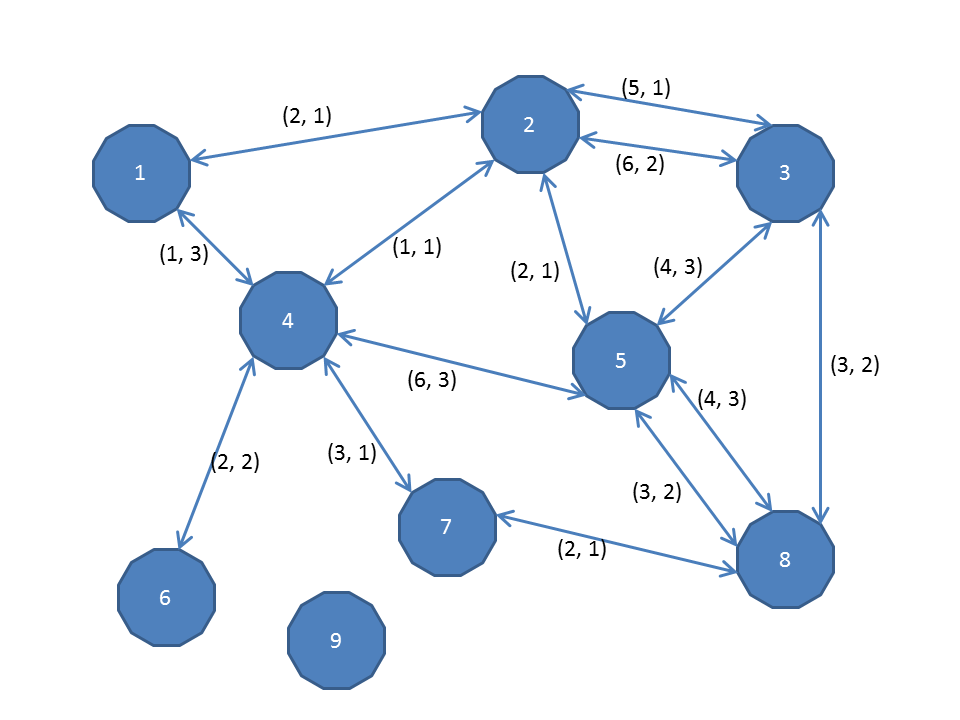
この時1-8, 3-7間のそれぞれの最小運賃は6, 5となる.
また,社長1と4, 9そしてあなたが知り合いになった時1の企業の路線が半額になる為,1-8, 3-7間のそれぞれの最小運賃は3, 3となる.
最後に1-9間の最小運賃を知りたいがそのような経路は無いのでNAとなる.
※線路と路線が激しく混同しそうなので落ち着いて文章を読むこと.