0752 - 凸多角形柱工業都市

時間制限 8 秒 / メモリ制限 512 MB / 得点 10 / Writer root / x 1 / 統計 /

誤差
1e-3
TLE
8sec
MLE
512MB
得点
10

問題

凸多角形柱工業都市 (Industrial Convex Pillar City, ICPC) はいくつかの凸多角形柱の形状をした建物からなる街である．あなたはこの街の中を現在地 $S$ から目的地 $T$ に向けて歩こうとしている．今日は日差しが強いので，出来る限りひなたを通らずに目的地へ向かいたい．あなたが立っている地点と太陽を一直線に結んだ線上に建物がある場合，あなたは建物の陰にいるので日差しを受けずにすむ．また，この街の建物の外周には全てひさしが付いているので，建物の外周に沿って歩いている間は，日が当たる縁に沿って歩いても日差しを受けることはない．あなたは建物の内部以外はこの街をどこでも自由に歩くことができる．

もっとも日差しを受けないように現在地から目的地まで歩いた時の，ひなたを歩く距離を出力するプログラムを作成しなさい．

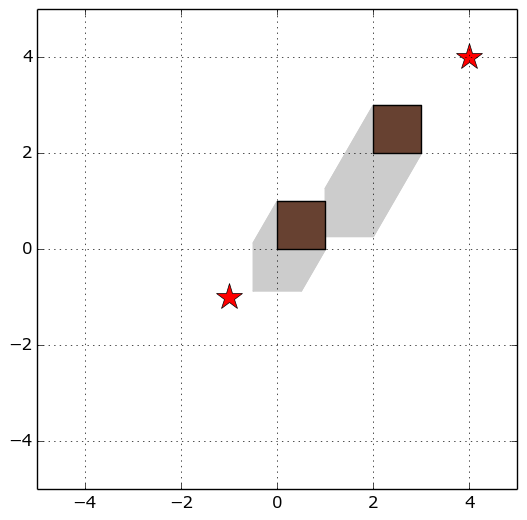
図E1: 第 $1$ インプットの場合

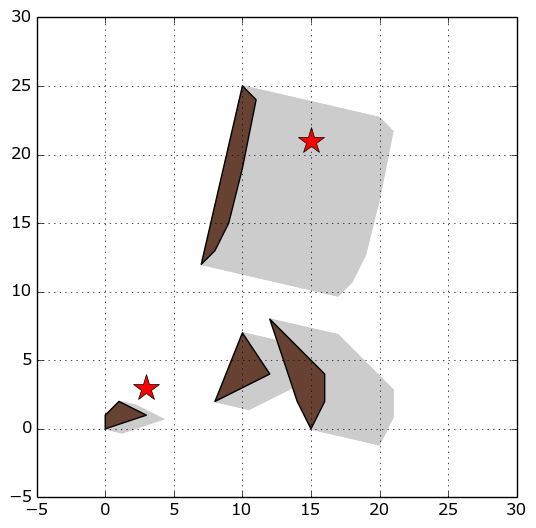
図E2: 第 $2$ インプットの場合

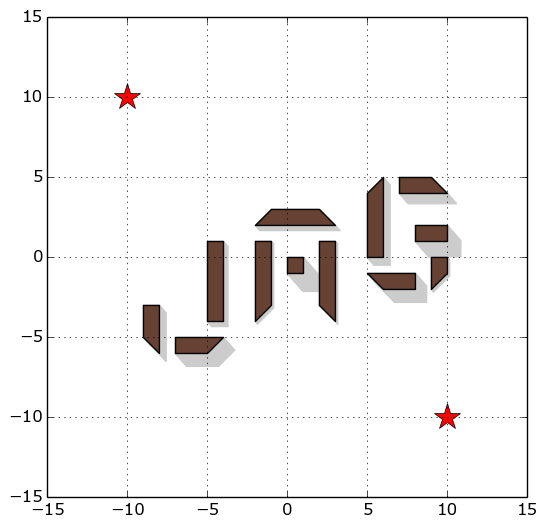
図E3: 第 $3$ インプットの場合

Input

入力は複数のデータセットからなる． データセットの個数は最大でも $30$ 個を超えない． 各データセットは次の形式で表される． 

$N$
$NV_1$ $H_1$ $X_{1,1}$ $Y_{1,1}$ $X_{1,2}$ $Y_{1,2}$ $\dots$ $X_{1,NV_1}$ $Y_{1,NV_1}$
$\dots$
$NV_N$ $H_N$ $X_{N,1}$ $Y_{N,1}$ $X_{N,2}$ $Y_{N,2}$ $\dots$ $X_{N,NV_N}$ $Y_{N,NV_N}$
$\theta$ $\phi$
$S_x$ $S_y$ $T_x$ $T_y$

$1$ 行目の $N$ は建物の数を表す．続く $N$ 行は各建物の形状を指定する．$NV_i$ は $i$ 番目の建物を上から見た多角形の頂点数，$H_i$ は $i$ 番目の建物の高さを表す．$X_{i, j}$ と $Y_{i, j}$ は $i$ 番目の建物を上から見た多角形の $j$ 番目の頂点の $x$ 座標と $y$ 座標を表す．頂点は反時計回りの順で与えられる．全ての建物は上から見ると凸多角形であり，建物の内部に他の建物があったり，頂点や辺が他の多角形と重なったりすることはない．続く行には太陽の方向を表す $\theta$ と $\phi$ が与えられ，$\theta$ は太陽の向きを $x$ の正の方向から反時計回りの角度で表し，$\phi$ は地平線からの太陽の仰角，すなわち太陽を見上げた時の視線の方向と地表面がなす角度を表す．ただし，太陽は無限遠にあり，移動中には位置を変えないものとする．続く行には現在地と目的地の座標， $(S_x, S_y)$ と $(T_x, T_y)$ が与えられる．

入力で与えられる数値は全て整数であり，以下の条件を満たす．

  • $1 \le N \le 100$
  • $3 \le NV_i \le 12$
  • $1 \le H_i \le 1{,}000$
  • $0 \le \theta \lt 360$
  • $0 \lt \phi \lt 90$

座標は全て $-1{,}000$ 以上 $1{,}000$ 以下である． 現在地と目的地は異なり，どちらも建物の内部及び外周には存在しない．

入力の終わりは，$1$ つのゼロからなる行で表される．

Output

各データセットについて，ひなたを歩く最短距離を $1$ 行に出力せよ．出力には $0.001$ を超える絶対誤差があってはならない．

Sample Input

2
4 1 0 0 1 0 1 1 0 1
4 2 2 2 3 2 3 3 2 3
60 45
-1 -1 4 4
4
4 1 0 0 3 1 1 2 0 1
3 2 10 7 8 2 12 4
6 8 7 12 8 13 9 15 10 19 11 24 10 25
5 4 16 2 16 4 12 8 14 2 15 0
167 38
3 3 15 21
12
4 3 -8 -3 -9 -3 -9 -5 -8 -6
4 5 -4 -5 -7 -5 -7 -6 -5 -6
4 2 -4 1 -5 1 -5 -4 -4 -4
4 1 -1 1 -2 1 -2 -4 -1 -3
4 2 2 3 -1 3 -2 2 3 2
4 1 3 1 2 1 2 -3 3 -4
4 7 1 0 0 0 0 -1 1 -1
4 4 9 5 7 5 7 4 10 4
4 3 6 5 5 4 5 0 6 0
4 5 8 -1 5 -1 6 -2 8 -2
4 1 10 0 9 0 9 -2 10 -1
4 6 10 2 8 2 8 1 10 1
131 78
-10 10 10 -10
0

Output for Sample Input

1.93185
7.87174
20.86840