0760 - devilswalk

問題

うくさんは横 $W \times$ 縦 $H$ マスからなる長方形の形をした街に住んでいます。 うくさんは $1$ 秒ごとに街の外に出ないように隣接する上下左右のいずれかのマスに移動します。

$N$ 個のマスには甜菜が埋まっていて、通ることができません。 うくさんは毎日†最高のメロンパン†をお散歩を兼ねてちょうど $T$ 秒間かけて買いに行きます。

うくさんは最初マス $(SX,SY)$ にいて、†最高のメロンパン†はマス $(GX,GY)$ にあるお店で売っています。 この街ではとても引っ越しが多いので、マス $(SX,SY)$ とマス $(GX,GY)$ はとても頻繁に変わります。

ところで、うくさんはお散歩の道順が一体何種類あるのか気になり始めてしまいました。

マス $(SX,SY)$ とマス $(GX,GY)$ のペアが $Q$ 個与えられるので、それぞれのペアについて、 ちょうどT秒間かけてマス $(SX,SY)$ からマス $(GX,GY)$ に移動する道順の数を求めてください。

求める数は非常に大きくなり得るので、$10^9+7$ で割った余りを答えてください。

ある二つの道順について、各 $k(1 \le k \le T)$ について、$k$ 番目に訪れた頂点が一致している時、 そしてその時に限りその二つの道順は同一であると定義します。

入力

$W$ $H$ $T$
$N$
$TX_1$ $TY_1$
$TX_2$ $TY_2$
$:$
$TX_N$ $TY_N$
$Q$
$SX_1$ $SY_1$ $GX_1$ $GY_1$
$SX_2$ $SY_2$ $GX_2$ $GY_2$
$:$
$SX_Q$ $SY_Q$ $GX_Q$ $GY_Q$

$1$ 行目には, マスの横の長さ $W$ と縦の長さ $H$、お散歩の時間 $T(1 \le W, H \le 16, 2 \le W \times H , 1 \le T \le 10^6)$ が与えられます。
$W \times H$ と $T$ は偶数であることが保証されています。

$2$ 行目には, 埋まっている甜菜の個数 $N(0 \le N \le W \times H - 2)$ が与えられます。

つづく $N$ 行のうち $i$ 行目には, $TX_i, TY_i(1 \le TX_i \le W, 1 \le TY_i \le H)$ が与えられます。 これは $i$ 番目の甜菜がマス $(TX_i, TY_i)$ に埋まっていることを意味します。
$i \ne j (1 \le i, j \le N)$ ならば $TX_i \ne TX_j$ または $TY_i \ne TY_j$ であることが保証されています。

$N+3$ 行目には, マス $(SX, SY)$ とマス $(GX, GY)$ のペアの個数 $Q(1 \le Q \le 10^4)$ が与えられます。

つづく $Q$ 行のうち $j$ 行目には, $SX_j, SY_j, GX_j, GY_j(1 \le SX_j, GX_j \le W, 1 \le SY_j, GY_j \le H)$ が与えられます。 これは $j$ 番目のペアがマス $(SX_j, SY_j)$ とマス $(GX_j, GY_j)$ であることを意味します。
マス $(SX_j, SY_j)$ とマス $(GX_j, GY_j)$ には甜菜が埋まっていないことが保証されます。

街の甜菜が埋まっていない各マスについて、必ず上下左右いずれかの方向には移動できることが保証されます。

出力

出力は $Q$ 行からなります。

$j(1 \le j \le Q)$ 行目にはマス $(SX_j, SY_j)$ からマス $(GX_j, GY_j)$ までちょうど $T$ 秒間で移動する道順の数を $10^9+7$ で割った余りを出力してください。

入出力例

入力例 1

5 4 4
1
2 2
2
1 1 3 3
1 1 5 1

出力例 1

2
1

街の様子は以下の図のようになります。

一つ目のペアについて、考えられる道順は

• $(1,1)$->$(1,2)$->$(1,3)$->$(2,3)$->$(3,3)$
• $(1,1)$->$(2,1)$->$(3,1)$->$(3,2)$->$(3,3)$

の二通りなので、道順の数は $2$ となります。

二つ目のペアについて、考えられる道順は

• $(1,1)$->$(2,1)$->$(3,1)$->$(4,1)$->$(5,1)$

の一通りなので、道順の数は $1$ となります。

入力例 2

5 4 2
3
1 3
2 2
3 1
2
1 1 1 2
1 1 5 1

出力例 2

0
0

街の様子は以下の図のようになります。

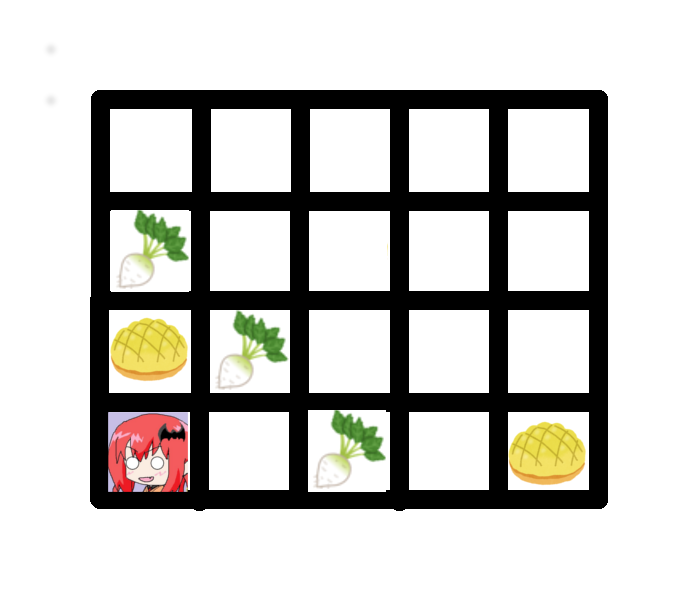
道順が存在しない場合もあります。
散歩の途中でメロンパン屋さんを通ったとしても、ちょうど $T$ 秒後にメロンパン屋さんにいない場合は道順としてカウントされないことに注意してください。

入力例 3

6 6 6
3
1 1
2 5
5 3
2
3 3 3 3
2 2 2 2

出力例 3

361
271

入力例 4

16 16 10000
0
1
1 1 16 16

出力例 4

810965164

$10^9+7$ で割った余りを出力してください。