問題
$N$ 頂点からなる木があります。 $N-1$ 本の辺はそれぞれ異なる $2$ つの頂点を双方向に結んでいます。
うくさんは, この木を掌握したいと考えました。
$M$ 個の操作の候補があります。 $i$ 回目の操作は以下を意味します。
- 頂点 $U_i$ と頂点 $V_i$ を結ぶ両端を含むパス上の頂点を全て掌握する。 ただし両端を含むパス上に, 既に掌握された頂点が $1$ 個以上あるとき, この操作は行えない。
ここでパスとは, $2$ つの頂点間を最短距離で移動するときの経路とします。
うくさんは $M$ 個の操作の候補のうちのいくつかを選んで, それらの操作を行うことができます。うくさんが掌握できる頂点数の最大値を求めてください。
入力
$N$ $M$
$A_1$ $B_1$
$A_2$ $B_2$
$:$
$A_{N-1}$ $B_{N-1}$
$U_1$ $V_1$
$U_2$ $V_2$
$:$
$U_M$ $V_M$
$1$ 行目には, 木の頂点数 $N(2 \le N \le 10^5)$ と操作の候補数 $M(1 \le M \le 2 \times 10^5)$ が与えられます。
つづく $N - 1$ 行のうち $i$ 行目には, $2$ つの整数 $A_i, B_i(1 \le A_i, B_i \le N, A_i \ne B_i)$ が与えられます。 これは, $i$ 番目の辺が頂点 $A_i$ と頂点 $B_i$ との間を双方向に結んでいることを意味します。 与えられるグラフは木であることが保証されます。
つづく $M$ 行のうち $i$ 行目には, $2$ つの整数 $U_i, V_i(1 \le U_i, V_i \le N)$ が与えられます。 これは $i$ 番目の操作で, 頂点 $U_i$ と頂点 $V_i$ を結ぶ両端を含むパス上の頂点を全て掌握することを意味します。
出力
$1$ 行に, 掌握できる頂点数の最大値を出力してください。
入出力例
入力例 1
7 5 3 4 5 4 6 5 2 7 1 5 5 7 1 3 7 2 6 6 7 6 5 4
出力例 1
7
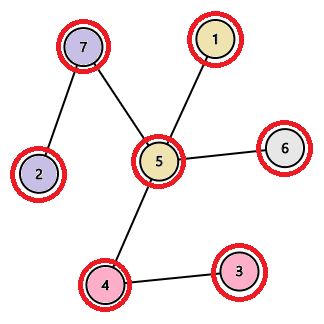
操作 $1, 2, 3$ を行うことで, 木の全ての頂点を掌握できます。
入力例 2
7 5 3 4 5 4 6 5 2 7 1 5 5 7 1 2 2 7 5 6 5 3 1 5
出力例 2
5
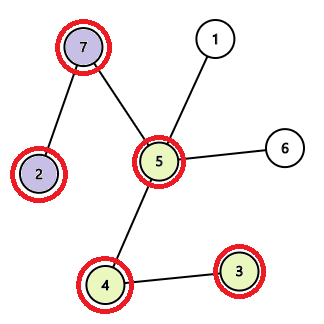
操作 $2, 4$ を行うことで $5$ 個の頂点を掌握できます。