Problem
モダンな庭園の設計者であるガーディナー氏は,自然の地形を活かすことにとても長けている. その設計法はユニークで,最初にまず池の位置を決め,自然の地形に手を加えずに池を設計する.
彼独特の手順で設計すると池の形は必ず簡単な縦横比の長方形になる. ガーディナー氏はまず,庭の用地の地図上に単位正方形のセルに分割する格子を描き,各セルに標高を記す. 彼の設計法では,池はいくつかのセルからなる長方形領域を占める. 領域の一番外側の各セルは,内部のどのセルよりも高くなくてはならない. たとえば,以下のグリッド状の地図(数値は標高を表す)では,灰色の領域(濃い灰色が一番外側のセル,薄い灰色が内部のセルを表す)に池を作ることができる. 一番外側のセルは最低でも高さが $3$ あり,内部のセルは最高でも高さが $2$ であることは,容易に見て取れるであろう.
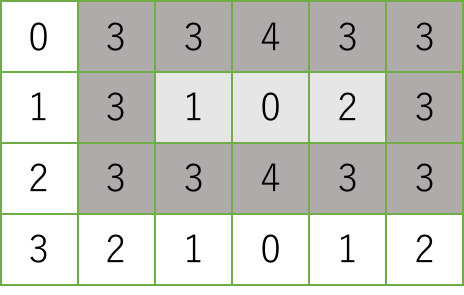
池を作る長方形領域は,内部セルを少なくとも一つ持つ必要がある. したがって,幅も奥行きも $3$ 以上でなければならない.
池の内部セルに水を注ぐと,水位が一番外側のセルの中で最も低いところに達するまで水を溜めることができる. さらに注ぎ続ければ,水は当然溢れ出てしまう. ガーディナー氏は,池の容量は大きければ大きいほど良いと考えている. ここで,池の容量とは,溜められる水の最大量のことである. たとえば,上の地図で灰色の領域に池を作った場合,池の容量は $(3 - 1) + (3 - 0) + (3 - 2) = 6$ になる. ここで,3 は一番外側のセルの中で最も低いものの標高であり,$1, 0, 2$ は内部セルの標高である. 単位正方形の各セルの標高が記されたグリッド状の地図を与えられた時,この用地に作れる池の最大容量を計算するプログラムを作成するのが,あなたの仕事である.
なお,以下のどちらの長方形領域も池にはならない. 左側の場合,右下隅のセルが内部セルより高くない. 右側の場合,真ん中のセルが一番外側のセルと同じ高さである.
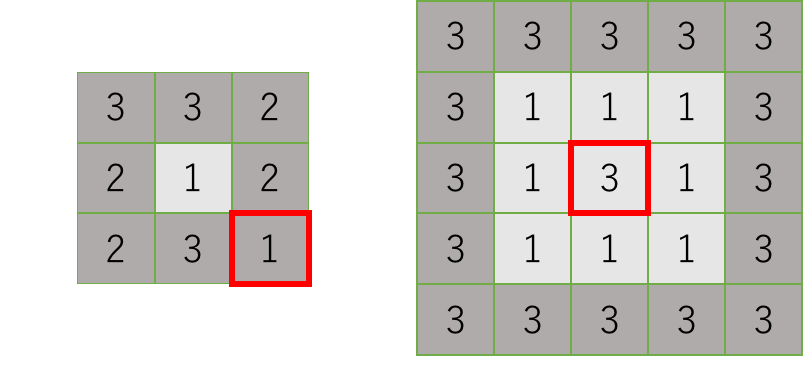
Input
入力は高々 $100$ 個のデータセットからなる. 各データセットは次の形式で表される.
$d$ $w$
$e_{1, 1}$ $\dots$ $e_{1, w}$
$\dots$
$e_{d, 1}$ $\dots$ $e_{d, w}$
最初の行の $d$ と $w$ はそれぞれ地図に示す庭の用地の奥行きと幅を表しており,$3$ 以上 $10$ 以下の整数である. 続く $d$ 行では,各行が空白文字 $1$ 個で区切られた $w$ 個の $0$ 以上 $9$ 以下の整数を含んでいる. この $d$ 行中 $y$ 番目の行の $x$ 番目の整数は,座標 $(x, y)$ の単位正方形のセルの標高である.
入力の終わりは,空白文字 $1$ 個で区切られたゼロ $2$ 個からなる行で表される.
Output
各データセットに対し,そのデータセットが示す庭の用地に作れる池のうち,最大容量のものの容量を $1$ 行に出力せよ. もし,池が作れない場合にはゼロを $1$ 行に出力せよ.
Sample Input
3 3 2 3 2 2 1 2 2 3 1 3 5 3 3 4 3 3 3 1 0 2 3 3 3 4 3 2 7 7 1 1 1 1 1 0 0 1 0 0 0 1 0 0 1 0 1 1 1 1 1 1 0 1 0 1 0 1 1 1 1 1 1 0 1 0 0 1 0 0 0 1 0 0 1 1 1 1 1 6 6 1 1 1 1 2 2 1 0 0 2 0 2 1 0 0 2 0 2 3 3 3 9 9 9 3 0 0 9 0 9 3 3 3 9 9 9 0 0
Output for the Sample Input
0 3 1 9